Schiefe Ebene: Eine Kiste mit der Masse...

Question

Eine Kiste mit der Masse 135kg wird mit konstanter Geschwindigkeit über eine 12m lange und 2,4m hohe schiefe

Ebene bei einer Reibungszahl my=0,25 zuerst über die gesamte Länge hinauf und anschließend wieder hinab gezogen.

a) Beerechnen Sie die Hangabtriebskraft und die Normalkraft.

b) Welche Kräfte sind für die Aufwärts- bzw. Abwärtsbewegung erforderlich?

c) Wir groß ist die insgesamt verrichtete Arbeit?

d) Wie lange dauert das Hochziehen mit einer Seilwinde der Nutzleistung 235W?

Answer 1

Vorgaben:
m=135 kg // Masse der Kiste
my=0,25 // Reibwert
h=2,4 m // Höhe der Ebene
l=12 m // Länge der Ebene
g=9,81N/kg=9,81m/s^2 // Ortsfaktor, Erdbeschleunigung
P=235 W // Antriebsleistung

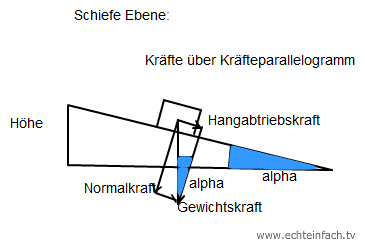
Berechnung:
alpha: h/l=sin(alpha); alpha=arcsin(h/l)=11,537°; // Winkel der Ebene
F_g=m*g=1324,35 N; // Gewichtskraft
F_H: sin(alpha)=F_H/F_g; F_H=F_g*sin(alpha)=F_g*h/l=264,87 N;Hangabtriebskraft; Merkhilfe: Da die Hangabtriebskraft mit abnehmendem Winkel kleiner wird, muss es sin(alpha)*F_g sein, da der Sinus bei 0° auch 0 ist.
F_N: cos(alpha)=F_N/F_g; F_N=cos(alpha)*F_g=cos(arcsin(h/l))=1297,59 N; // Normalkraft
F_R=F_N*my=324,40 N; // Reibkraft
F_auf=F_H+F_R=589,27 N; // Kraft um die Kiste nach oben ziehen zu können bei konstanter Geschwindigkeit
F_ab=-F_H+F_R=59,53 N; // Kraft um die Kiste nach unten zu ziehen; positives Vorzeichen -> Kiste rutscht nicht
W=F_auf*l+F_ab*l=7785,6 J; // verrichtete Arbeit; es gilt W=F*s (Arbeit = Kraft * Weg); 1Nm=1Ws=1J
t=W/P=33,1 s; // Zeitdauer; idealisierte Vorstellung; es gilt W=P*t (Arbeit = Leistung * Zeit);

Comments

Warum nimmst du den Sinus? Man muss doch hier mit Tangens rechnen

tan_alpha=Gegenkathete/Ankathete

---

l ist halt die Länge der (schiefen) Ebene (die Hypotenuse). Daher ist Sinus ok.

---

stimmt, so kann man es auch sehen. danke