Ersatzquellenverfahren aus der Elektrotechnik.

Question

Ich weiß, passt nicht 100%ig in das Forum - aber vielleicht kennt sich ja wer damit aus.

Comments

das sieht relativ aufwendig aus kennst du dich denn kein bisschen damit aus ?

als erstes würde ich die stormquellen in spannungsquellen umwandeln und zusammenfassen. anschliessend nimmst du R6 aus der schaltung und fasst alle widerstände zusammen. das ist der innenwiderstand der ersatzquelle.

danach kannst du die spannung Uq der ersatzquelle bestimmen. das ist die spannung die an den klemmen anliegt an der du R6 rausgenommen hast. hier kannst du eine maschengleichung bilden und Uq ausrechnen.

---

umzeichnen hilft oft enorm!

---

Man muss halt nur jemanden finden, der das für einen erledigt ...

---

@pleindespoir: Findest du das wirklich so trivial?

---

Nicht trivial - aber es wäre halt schön gewesen, wenn der Fragesteller mal einen Versuch Eigenaktivität gestartet hätte.

Oder zumindest eine Rückfrage, aber warten bis jemandem langweilig ist und es fertigrechnet, geht ja auch oft.

Answer 1

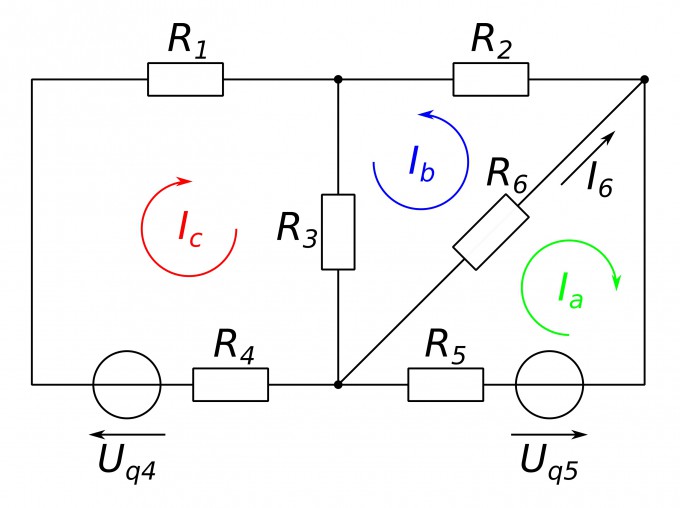
1. Wandle die Stromquellen in Spannungsquellen um:

U_q4 = R₄ · I_q4
U_q5 = R₅ · I_q5


2. Berechne die Maschenströme I_a und I_b, indem du folgendes Gleichungssystem löst:

Masche a:  (R₅ + R₆) · I_a  +  R₆ · I_b  =  R₅ · I_q5
Masche b:  R₆ · I_a  +  (R₂ + R₃ + R₆) · I_b  +  R₃ · I_c  =  0
Masche c:  R₃ · I_b  +  (R₁ + R₃ + R₄) · I_c  =  - R₄ · I_q4


3. Berechne die Stromstärke I₆, welche durch den Widerstand R₆ fließt:

I₆ = I_a + I_b

$${ I }_{ 6 }=\frac { \left( { I }_{ 4 }{ R }_{ 3 }{ R }_{ 4 }+{ I }_{ 5 }\left( { R }_{ 1 }\left( { R }_{ 2 }+{ R }_{ 3 } \right) +{ R }_{ 2 }\left( { R }_{ 3 }+{ R }_{ 4 } \right) +{ R }_{ 3 }{ R }_{ 4 } \right) \right) { R }_{ 5 } }{ { R }_{ 1 }\left( \left( { R }_{ 2 }+{ R }_{ 3 } \right) \left( { R }_{ 5 }+{ R }_{ 6 } \right) +{ R }_{ 5 }{ R }_{ 6 } \right) +{ R }_{ 2 }\left( { R }_{ 3 }+{ R }_{ 4 } \right) \left( { R }_{ 5 }+{ R }_{ 6 } \right) +{ R }_{ 3 }\left( { R }_{ 4 }\left( { R }_{ 5 }+{ R }_{ 6 } \right) +{ R }_{ 5 }{ R }_{ 6 } \right) +{ R }_{ 4 }{ R }_{ 5 }{ R }_{ 6 } }$$

4. Berechne die Leerlaufspannung der Ersatzspannungsquelle:
$${ U }_{ e6 }=\lim _{ { R }_{ 6 }\rightarrow \infty }{ { U }_{ 6 } } =\lim _{ { R }_{ 6 }\rightarrow \infty }{ { R }_{ 6 }{ I }_{ 6 } }$$
$${ U }_{ e6 }=\frac { \left( { I }_{ 4 }{ R }_{ 3 }{ R }_{ 4 }+{ I }_{ 5 }\left( { R }_{ 1 }\left( { R }_{ 2 }+{ R }_{ 3 } \right) +{ R }_{ 2 }\left( { R }_{ 3 }+{ R }_{ 4 } \right) +{ R }_{ 3 }{ R }_{ 4 } \right) \right) { R }_{ 5 } }{ { R }_{ 1 }\left( { R }_{ 2 }+{ R }_{ 3 }+{ R }_{ 5 } \right) +{ R }_{ 2 }\left( { R }_{ 3 }+{ R }_{ 4 } \right) +{ R }_{ 3 }\left( { R }_{ 4 }+{ R }_{ 5 } \right) +{ R }_{ 4 }{ R }_{ 5 } }$$

5. Berechne die Kurzschlußstromstärke der Ersatzspannungsquelle:
$${ I }_{ e6 }=\lim _{ { R }_{ 6 }\rightarrow 0 }{ { I }_{ 6 } }$$
$${ I }_{ e6 }=\frac {{ I }_{ 4 }{ R }_{ 3 }{ R }_{ 4 }+{ I }_{ 5 }\left( { R }_{ 1 }\left( { R }_{ 2 }+{ R }_{ 3 } \right) +{ R }_{ 2 }\left( { R }_{ 3 }+{ R }_{ 4 } \right) +{ R }_{ 3 }{ R }_{ 4 } \right) }{ { R }_{ 1 }\left( { R }_{ 2 }+{ R }_{ 3 } \right) +{ R }_{ 2 }\left( { R }_{ 3 }+{ R }_{ 4 } \right) +{ R }_{ 3 }{ R }_{ 4 }}$$

6. Berechne den Innenwiderstand der Ersatzspannungsquelle:
$${ R }_{ e6 }=\frac { { U }_{ e6 } }{ { I }_{ e6 } }$$
$${ R }_{ e6 }=\frac { \left( { R }_{ 1 }\left( { R }_{ 2 }+{ R }_{ 3 } \right) +{ R }_{ 2 }\left( { R }_{ 3 }+{ R }_{ 4 } \right) +{ R }_{ 3 }{ R }_{ 4 } \right) { R }_{ 5 } }{ { R }_{ 1 }\left( { R }_{ 2 }+{ R }_{ 3 }+{ R }_{ 5 } \right) +{ R }_{ 2 }\left( { R }_{ 3 }+{ R }_{ 4 } \right) +{ R }_{ 3 }\left( { R }_{ 4 }+{ R }_{ 5 } \right) +{ R }_{ 4 }{ R }_{ 5 } }$$