Hallo liebe Forenmitglieder,
ich hoffe, dass mir jemand mit physikalischen und mathematischen Verständnis weiterhelfen kann:
ich soll für einen Physikversuch eine Fehlerrechnung machen: 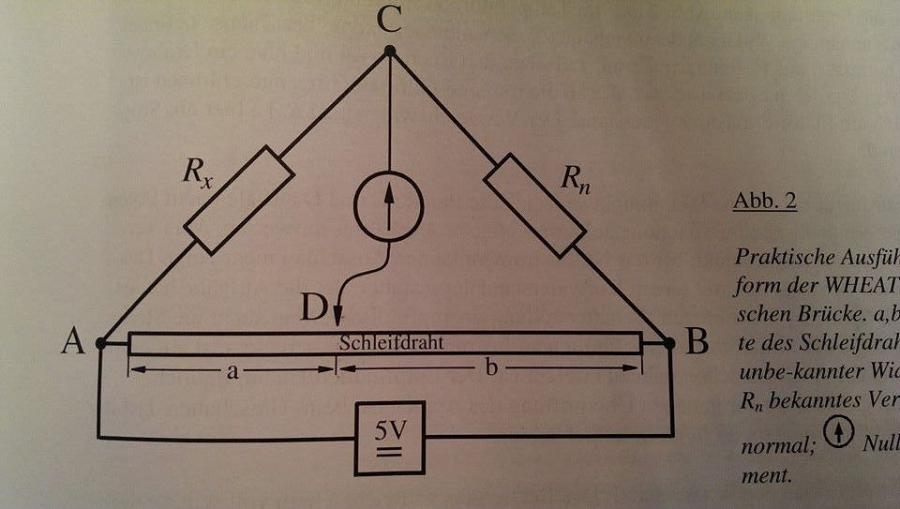
Δa: Der Ablesefehler für a liegt bei etwa 0,1 cm. Der kleinste Fehler für den Quotienten a/b ergibt sich, wenn beide Zahlen gleich sind.
ΔRn: Der Fehler für Rn beträgt etwa 0,1 Ω.
ΔT: Der Fehler beim Ablesen der Temperatur liegt bei etwa 0,2
Die restlichen Werte a l Rn habe ich durch meinen Versuch erhalten.
Uns wurde folgende Formel gegeben:
ΔRx / Rx = ΔRn/Rn + l/a(l-a) * Δa
Nun wird nach ΔRx aufgelöst und differenziert und man erhält:
ΔRx = wurzel aus (dRx /dRn * ΔRn)² + (dRx/da*Δa)²
= wurzel aus (a/l-a*ΔRn)² + (Rn*(l-2a)/(l*a)² * Δa)²
Aus dieser Gleichung lässt sich nun für jede Einzelmessung der Maximalfehler berechnen:
ΔRx(rel.) = ΔRx/Rx *100
Mir ist nicht klar, warum ich hier differenzieren muss? Reicht es nicht einfach nach ΔRx umzustellen?