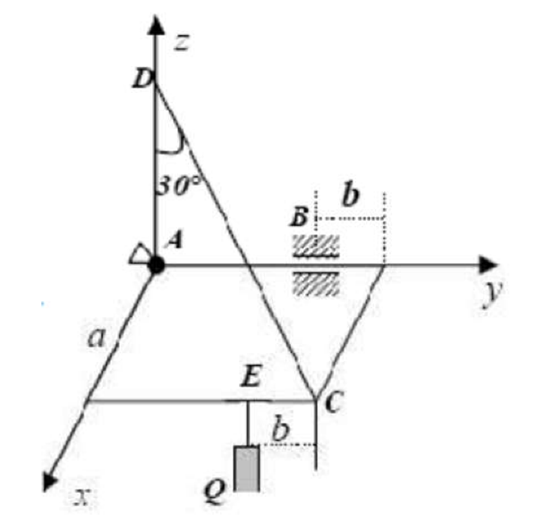
Aufgabe: Une plaque carrée
Eine quadratische Platte mit der Seitenlänge „a“ und dem Gewicht „P“ ist mittels eines Kugelgelenks in Punkt „A“ und eines Zylindergelenks in Punkt „B“ an einer Wand befestigt.
Ein masseloses, dehnungsfreies Seil „CD“ hält die Platte in horizontaler Position.
Eine Last „Q“ = 2P ist an Punkt „E“ der Platte aufgehängt.
Die gegebenen Parameter sind: b = a/3 ; α = 30°.
Bestimmen Sie die Auflagerkräfte in den Gelenken A und B sowie die Seilspannung als Funktion (Abhängigkeit) von „a“ und „P“. (und deren Beträge)
Problem/Ansatz:
Statik: Wie lauten die Koordinaten der Punkte „B“, „C“, „D“ und „E“?
Den Lösungsweg weiter kann ich via Statik mit den richtigen Koordinaten bewältigen.
Ich habe an folgenden Koordinaten gedacht:
A (0 / 0 / 0) ; B (0 / b / 0) = (0 / (a/3) / 0) ; C (a / b / 0) = (a / (a/3) / 0) ;
D (0 /0 / zD) mit zD = a. cos (30°) ; E (a / 0 / 0) und G ((a/2) / (a/2) / 0) = Schwerpunkt der Platte,
aber stimmen diese überhaupt?
Dann habe ich weiter die Vektoren der angreifenden Kräfte als Folgendes überlegt:
Gewicht P der Platte: Fp ( 0 / 0 / -P) angreifend in „G“ ;
Last „Q“: Fq (0 / 0 / -Q) = (0 / 0/ -2P) angreifend in „E“ ;
Seilkraft Fs = ? gesucht: wirkt entlang „CD“ ,
aber stimmen diese überhaupt?
Zusätzlich die Reaktionskräfte:
1.) Kugelgelenk „A“ lässt Rotation in alle Richtungen FA (FAx / FAy / FAz) => 3 unbekannte Kräfte
2.) Zylindergelenk „B“ erlaubt Rotation in 2 Richtungen FB (FBx / 0 / FBz) => 2 unbekannte Kräfte
3.) Seil „CD“ in eine Richtung Fs = ? => 1 unbekannte Kraft
Total 6 unbekannte Kräfte, aber stimmt das überhaupt?