Aufgabe:
Problem/Ansatz:
Text erkannt:
Aufgabe 1
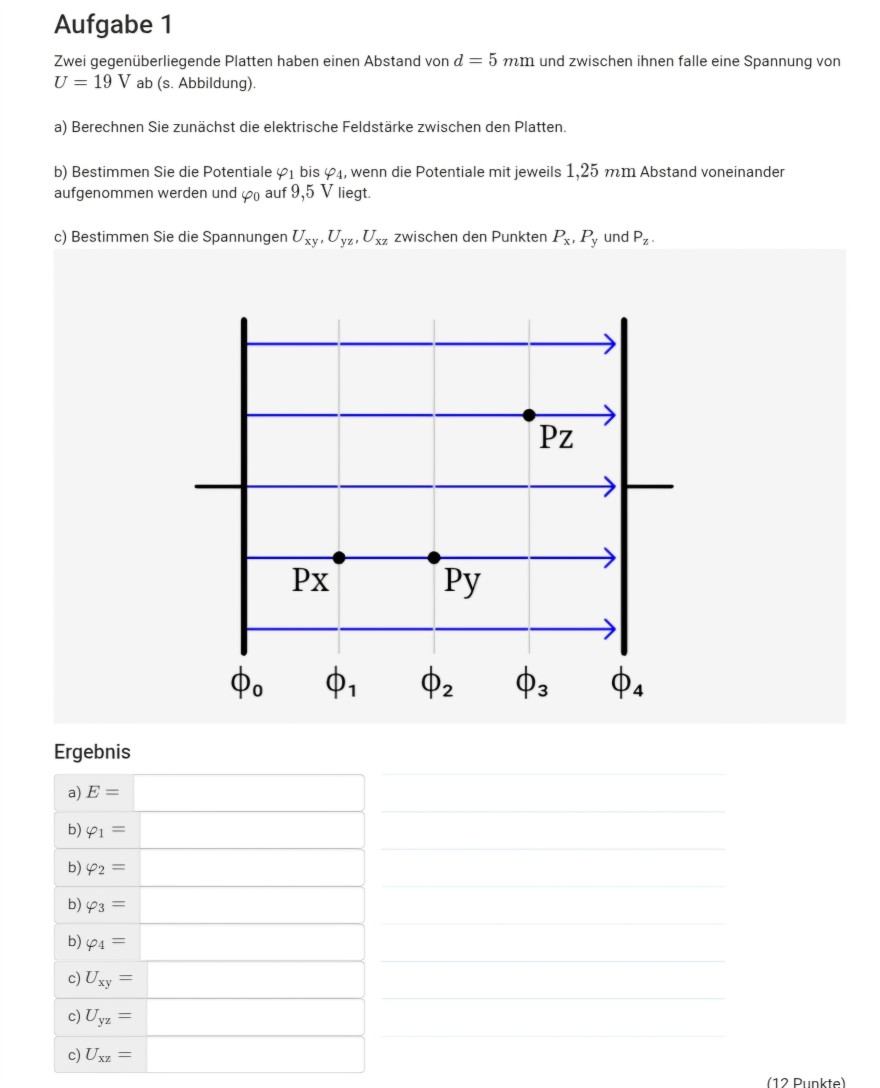
Zwei gegenüberliegende Platten haben einen Abstand von \( d=5 m \mathrm{~m} \) und zwischen ihnen falle eine Spannung von \( U=19 \mathrm{~V} \) ab (s. Abbildung).
a) Berechnen Sie zunächst die elektrische Feldstärke zwischen den Platten.
b) Bestimmen Sie die Potentiale \( \varphi_{1} \) bis \( \varphi_{4} \), wenn die Potentiale mit jeweils \( 1,25 \mathrm{~mm} \) Abstand voneinander aufgenommen werden und \( \varphi_{0} \) auf \( 9,5 \mathrm{~V} \) liegt.
c) Bestimmen Sie die Spannungen \( U_{\mathrm{xy}}, U_{\mathrm{yz}}, U_{\mathrm{xz}} \) zwischen den Punkten \( P_{\mathrm{x}}, P_{\mathrm{y}} \) und \( \mathrm{P}_{\mathrm{z}} \).
Ergebnis
a) \( E= \)
b) \( \varphi_{1}= \)
b) \( \varphi_{2}= \)
b) \( \varphi_{3}= \)
b) \( \varphi_{4}= \)
c) \( U_{x y}= \)
c) \( U_{y z}= \)
c) \( U_{\mathrm{xz}}= \)

Text erkannt:
Aufgabe 2
Die Metallplatten eines Kondensators, der mit Luft gefüllt ist, werden auf eine Spannung von \( U=82 \mathrm{~V} \) aufgeladen. Der Plattenabstand betrage \( d=3 \mathrm{~mm} \) und eine Platte habe die Fläche von \( 108 \mathrm{~cm}^{2} \). Die Spannungsquelle wird nur zur Aufladung angeschlossen und danach wieder entfernt. Eine Selbstentladung des Kondensators kann vernachlässigt werden.
a) Berechnen Sie die Feldstärke des homogenen elektrischen Feldes zwischen den Platten.
b) Welche Ladungsmenge befindet sich auf einer Platte?
c) Wie groß müssen zwei rechteckige Platten sein, wenn die Feldstärke doppelt so groß sein soll und wenn für das Verhältnis von Breite und Höhe des Rechtecks gilt, dass die Höhe \( =5 \cdot \) Breite ist. Die Ladung sei identisch wie in Aufgabe b)
Ergebnis
a) \( E=2733,33 \mathrm{~V} / \mathrm{m} \)
b) \( Q=2,61 \mathrm{nC} \)
\( 2733,33 \frac{\mathrm{~V}}{\mathrm{~m}} \)
c) Breite \( =3,29 \mathrm{~cm} \)
\( 3,29 \mathrm{~cm} \)
c) Höhe \( =16,45 \mathrm{~cm} \)
\( 16,45 \mathrm{~cm} \)
(9 Punkte)
Aufgabe 3
Die Metallplatten eines Plattenkondensators, deren Zwischenraum vollständig mit einem unbekannten Dielektrikum gefüllt sind, werden auf eine Spannung von \( U=37 \mathrm{~V} \) aufgeladen. Der Plattenabstand betrage \( d=4 \mathrm{~mm} \) und eine Platte habe die Fläche von \( 97 \mathrm{~cm}^{2} \). Die Ladung beträgt \( Q=10^{-8} \mathrm{C} \). Die Spannungsquelle wird nur zur Aufladung angeschlossen und danach wieder entfernt. Eine Selbstentladung des Kondensators kann vernachlässigt werden.
Berechnen Sie die Permittivität \( \left(\epsilon=\epsilon_{0} \cdot \epsilon_{\mathrm{r}}\right) \) des Dielektrikums. (Eingabe mit Einheit \( \mathrm{As} / \mathrm{Vm} \) ).
Ergebnis
\( \epsilon=1,11^{*} 10^{\wedge}-10 \mathrm{As} / \mathrm{Vm} \)
\( 1,11 \cdot 10^{-10} \frac{\mathrm{~A} \cdot \mathrm{~s}}{\mathrm{~V} \cdot \mathrm{~m}} \)
Sind Aufgabe 2 und 3 so richtig?
Bei Aufgabe 1 weiß ich gar nicht, wie ich anfangen soll.