Aufgabe:
Herleitung der Bellzustände
Problem/Ansatz:
Man hat ja die Definition der vier Bell-Zustände:
\[|\Phi^{\pm}\rangle = \frac{|00\rangle \pm |11\rangle}{\sqrt{2}}, |\Psi^{\pm}\rangle = \frac{|01\rangle \pm |10\rangle}{\sqrt{2}}\]
Ich bin gerade dabei die Herleitung zu berechnen, aber Ich weiß nicht genau ob ich es hier richtig berechnet habe. Kann mal jemand rüberschauen?
Danke im voraus :3
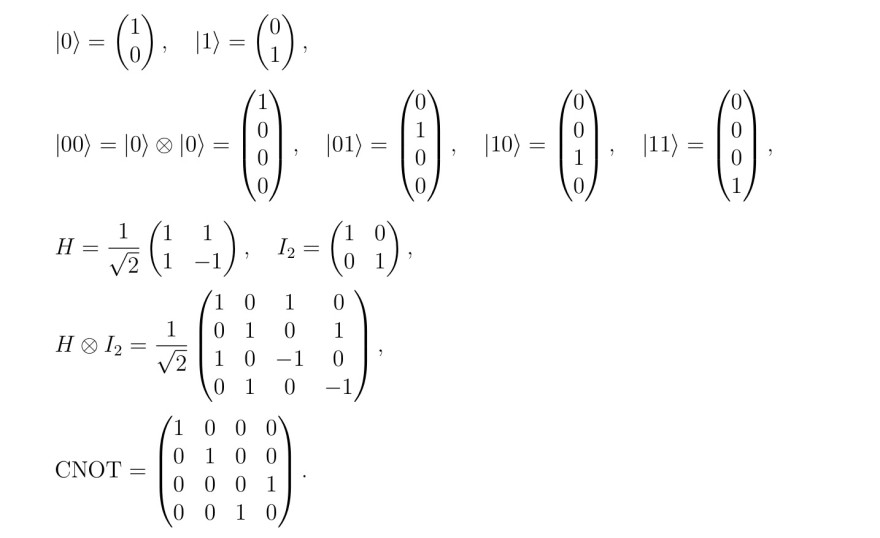
Text erkannt:
\( \begin{array}{l}|0\rangle=\binom{1}{0}, \quad|1\rangle=\binom{0}{1} \\ |00\rangle=|0\rangle \otimes|0\rangle=\left(\begin{array}{l}1 \\ 0 \\ 0 \\ 0\end{array}\right), \quad|01\rangle=\left(\begin{array}{l}0 \\ 1 \\ 0 \\ 0\end{array}\right), \quad|10\rangle=\left(\begin{array}{l}0 \\ 0 \\ 1 \\ 0\end{array}\right), \quad|11\rangle=\left(\begin{array}{l}0 \\ 0 \\ 0 \\ 1\end{array}\right) \\ H=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1 & 1 \\ 1 & -1\end{array}\right), \quad I_{2}=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right) \\ H \otimes I_{2}=\frac{1}{\sqrt{2}}\left(\begin{array}{cccc}1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1\end{array}\right) \\ \mathrm{CNOT}=\left(\begin{array}{llll}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0\end{array}\right)\end{array} \)

Text erkannt:
\( \begin{array}{l}\left(H \otimes I_{2}\right)|00\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{l}1 \\ 0 \\ 1 \\ 0\end{array}\right)=\frac{|00\rangle+|10\rangle}{\sqrt{2}}, \\ \mathrm{CNOT} \frac{|00\rangle+|10\rangle}{\sqrt{2}}=\frac{|00\rangle+|11\rangle}{\sqrt{2}}=\left|\Phi^{+}\right\rangle \\ \left(H \otimes I_{2}\right)|01\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{l}0 \\ 1 \\ 0 \\ 1\end{array}\right)=\frac{|01\rangle+|11\rangle}{\sqrt{2}}, \\ \mathrm{CNOT} \frac{|01\rangle+|11\rangle}{\sqrt{2}}=\frac{|01\rangle+|10\rangle}{\sqrt{2}}=\left|\Psi^{+}\right\rangle, \\ \left(H \otimes I_{2}\right)|10\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1 \\ 0 \\ -1 \\ 0\end{array}\right)=\frac{|00\rangle-|10\rangle}{\sqrt{2}}, \\ \mathrm{CNOT} \frac{|00\rangle-|10\rangle}{\sqrt{2}}=\frac{|00\rangle-|11\rangle}{\sqrt{2}}=\left|\Phi^{-}\right\rangle, \\ \left(H \otimes I_{2}\right)|11\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{c}0 \\ 1 \\ 0 \\ -1\end{array}\right)=\frac{|01\rangle-|11\rangle}{\sqrt{2}}, \\ \mathrm{CNOT} \frac{|01\rangle-|11\rangle}{\sqrt{2}}=\frac{|01\rangle-|10\rangle}{\sqrt{2}}=\left|\Psi^{-}\right\rangle .\end{array} \)
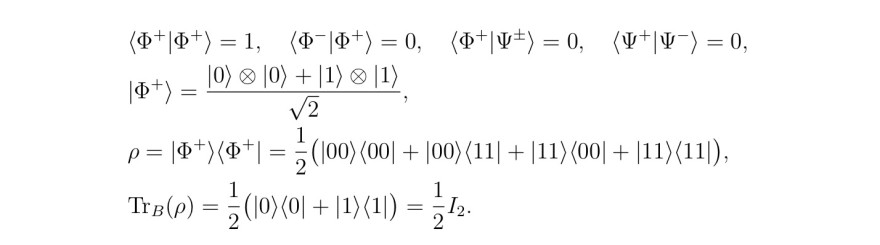
Text erkannt:
\( \begin{array}{l}\left\langle\Phi^{+} \mid \Phi^{+}\right\rangle=1, \quad\left\langle\Phi^{-} \mid \Phi^{+}\right\rangle=0, \quad\left\langle\Phi^{+} \mid \Psi^{ \pm}\right\rangle=0, \quad\left\langle\Psi^{+} \mid \Psi^{-}\right\rangle=0, \\ \left|\Phi^{+}\right\rangle=\frac{|0\rangle \otimes|0\rangle+|1\rangle \otimes|1\rangle}{\sqrt{2}}, \\ \rho=\left|\Phi^{+}\right\rangle\left\langle\Phi^{+}\right|=\frac{1}{2}(|00\rangle\langle 00|+|00\rangle\langle 11|+|11\rangle\langle 00|+|11\rangle\langle 11|), \\ \operatorname{Tr}_{B}(\rho)=\frac{1}{2}(|0\rangle\langle 0|+|1\rangle\langle 1|)=\frac{1}{2} I_{2} .\end{array} \)

Text erkannt:
\( \begin{array}{l} X=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right), \quad Z=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right), \quad Y=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \\ \left(Z \otimes I_{2}\right)\left|\Phi^{+}\right\rangle=\left|\Phi^{-}\right\rangle, \quad\left(X \otimes I_{2}\right)\left|\Phi^{+}\right\rangle=\left|\Psi^{+}\right\rangle, \\ \left(i Y \otimes I_{2}\right)\left|\Phi^{+}\right\rangle=\left|\Psi^{-}\right\rangle . \end{array} \)
\( U_{\mathrm{inv}}=\left(H \otimes I_{2}\right) \mathrm{CNOT}, \quad U_{\mathrm{inv}}\left|\Phi^{+}\right\rangle=|00\rangle, U_{\mathrm{inv}}\left|\Psi^{+}\right\rangle=|01\rangle, U_{\mathrm{inv}}\left|\Phi^{-}\right\rangle=|10\rangle, U_{\mathrm{inv}}\left|\Psi^{-}\right\rangle=|11\rangle . \)
\( \begin{array}{l} \operatorname{CNOT}\left(H \otimes I_{2}\right)|00\rangle=\left|\Phi^{+}\right\rangle, \\ \operatorname{CNOT}\left(H \otimes I_{2}\right)|01\rangle=\left|\Psi^{+}\right\rangle, \\ \operatorname{CNOT}\left(H \otimes I_{2}\right)|10\rangle=\left|\Phi^{-}\right\rangle, \\ \operatorname{CNOT}\left(H \otimes I_{2}\right)|11\rangle=\left|\Psi^{-}\right\rangle . \end{array} \)
\( \left|\Phi^{ \pm}\right\rangle=\frac{|00\rangle \pm|11\rangle}{\sqrt{2}}, \quad\left|\Psi^{ \pm}\right\rangle=\frac{|01\rangle \pm|10\rangle}{\sqrt{2}} \)