Aufgabe:
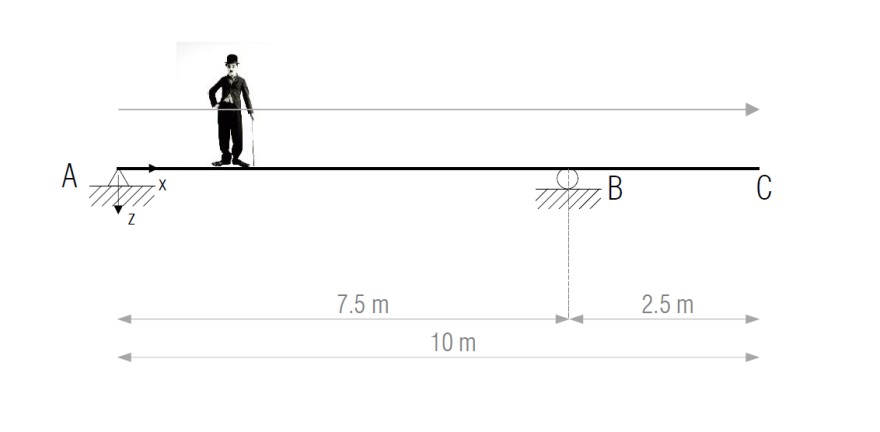
Ein 10 m langer Holzbalken hat ein Eigengewicht von 70 kg. Er ist gelagert als Einfacher Balken mit Kragarm gemäss Skizze.
Eine 80 kg schwere Person geht von A nach B und dann weiter in Richtung C.
Wie weit von A befindet sich die Person, wenn:
a) die Auflagerreaktion in A gerade doppelt so gross ist wie in B?
Falls A eine Stütze 10x10 cm wäre, wie gross sind die Normalspannungen?
b) die Auflagerreaktionen in A und B gleich gross sind?
c) der Balken zu kippen beginnt (falls A keine abhebenden Kräfte aufnehmen kann)?
Problem/Ansatz:
Bisher habe ich die vertikalen Kräfte (Person + Balken) berechnet, aber ich weiss nicht, wie ich vorgehen soll, ich weiss auch, dass ich ein Momentgleichgewicht (=0) berechnen muss. Ich habe keine Ahnung, wie ich vorgehen soll, es würde mir vielleicht helfen, auch nur die Formeln zu erhalten, die ich verwenden soll oder eine Erklärung, wie ich die Übung Schritt für Schritt berechnen kann.
Vielen Dank im Voraus für eure Unterstützung und Hilfsbereitschaft.