Text erkannt:
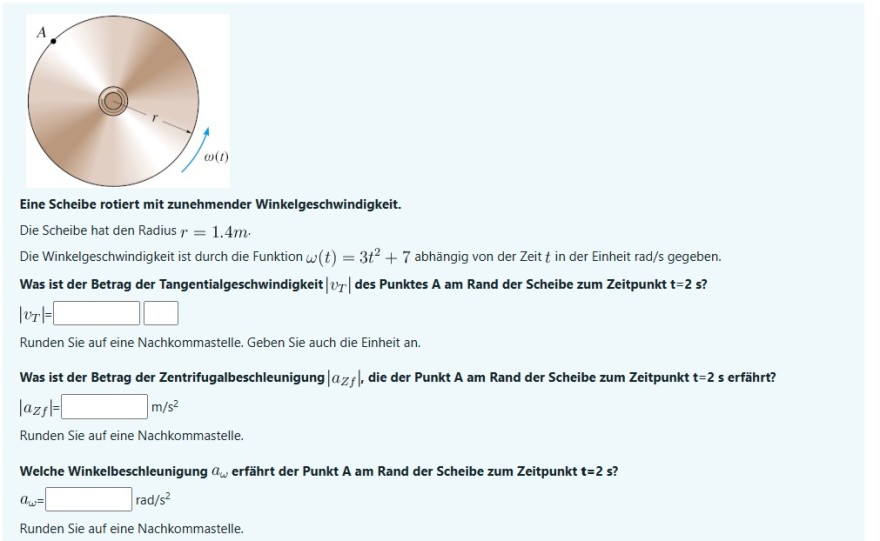
Eine Scheibe rotiert mit zunehmender Winkelgeschwindigkeit.
Die Scheibe hat den Radius \( r=1.4 m \).
Die Winkelgeschwindigkeit ist durch die Funktion \( \omega(t)=3 t^{2}+7 \) abhängig von der Zeit \( t \) in der Einheit rad/s gegeben.
Was ist der Betrag der Tangentialgeschwindigkeit \( \left|v_{T}\right| \) des Punktes A am Rand der Scheibe zum Zeitpunkt \( \mathbf{t}=\mathbf{2} \mathbf{s} \) ?
\( \left|v_{T}\right|= \)
Runden Sie auf eine Nachkommastelle. Geben Sie auch die Einheit an.
Was ist der Betrag der Zentrifugalbeschleunigung \( \left|a_{Z f}\right| \), die der Punkt A am Rand der Scheibe zum Zeitpunkt \( \mathbf{t}=2 \mathrm{~s} \) erfährt?
\( \left|a_{Z f}\right|=\square \mathrm{m} / \mathrm{s}^{2} \)
Runden Sie auf eine Nachkommastelle.
Welche Winkelbeschleunigung \( a_{\omega} \) erfährt der Punkt A am Rand der Scheibe zum Zeitpunkt t=2 s?
\( a_{\omega}=\square \mathrm{rad} / \mathrm{s}^{2} \)
Runden Sie auf eine Nachkommastelle.

Text erkannt:
Was ist der Betrag der Tangentialbeschleunigung \( \left|a_{T}\right| \), die der Punkt A am Rand der Scheibe zum Zeitpunkt t=2 s erfährt? \( \left|a_{T}\right|=\square \mathrm{m} / \mathrm{s}^{2} \)
Runden Sie auf eine Nachkommastelle.
Vielen Dank für den Lösungsansatz