Hallo :-)
Ich gehe mal davon aus, dass \(U=50V\) die Kondensatorspannung und \(U_b=1206V\) die Beschleunigungsspannung ist.
Die Ortsfunktion lautet, wie du schon richtig geschrieben hast \(y(x)=\frac{1}{4}\cdot \frac{U}{d}\cdot \frac{1}{U_b}\cdot x^2\), (mit \(0\leq x\leq s\)). Diese beschreibt die Ablenkung eines Elektrons, innerhalb des elektrischen Feldes (der Brown'schen Röhre).
Eingesetzt ergibt das
$$ y_1=y(0.035m)=\frac{1}{4}\cdot \frac{50V}{0.0025m}\cdot \frac{1}{1206V}\cdot (0.035m)^2\approx 5.08\cdot 10^{-3}m. $$
Gesamtablenkung
Beim Verlassen des Feldes bewegt sich dein Elektron auf einer Geraden
\(g(x)=\underbrace{m\cdot (x-s)}_{=y_2}+y_1\), (mit \(s\leq x\)) weiter:
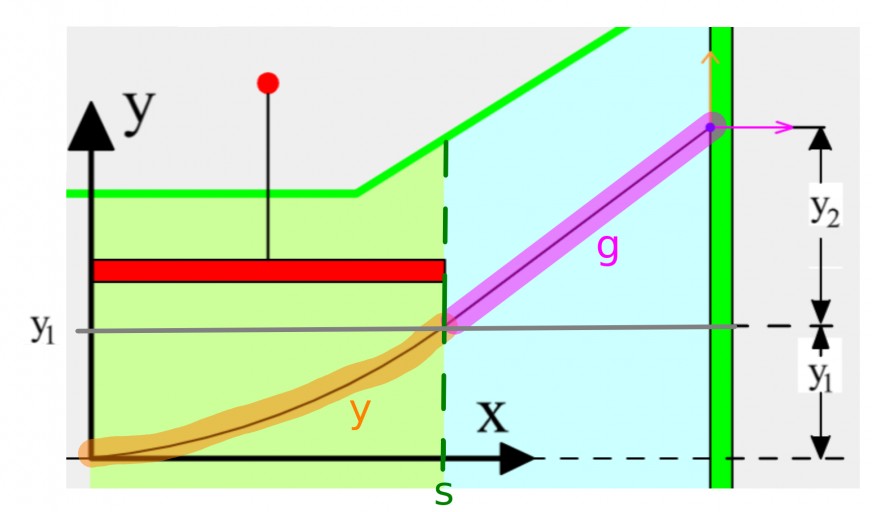
Dabei ist der Anstieg \(m\) dieser Geraden gleich dem Anstieg auf dem Parabelast an der Stelle \(s\). Also brauchst du jetzt die erste Ableitung von der Ortsfunktion im elektrischen Feld, also \(y'\)
Also lautet deine Geradenfunktion \(g(x)=\underbrace{y'(s)\cdot (x-s)}_{=y_2}+y_1\).