Wie errechnet man die Reibung und Gleitreibung auf schiefer Ebene?

Question

Aufgabe:

Eine Kiste mit einer Masse von 15 Kg wird einer Ebene mit eine Steigung von 30° auf der Horizontalen losgelassen und beschleunigt mit 0,3 m/s^2

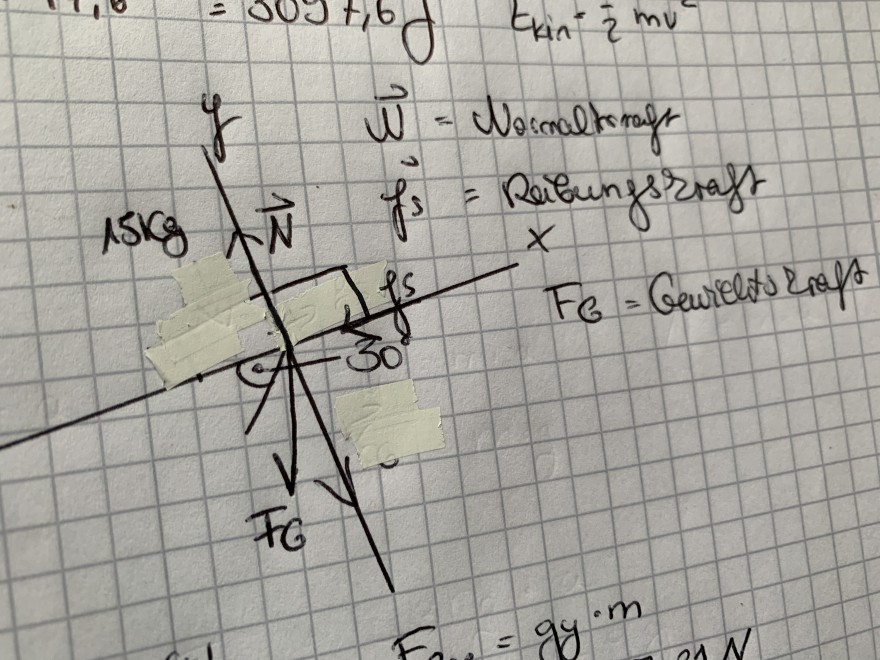
A) Fertigen sie eine Skizze an und zeichnen sie die Reibungskraft, die Gewichtskraft und die Gesamtkraft ein. Kennzeichnen sie ebenso die komponenten der Gewichtskraft entlang der Ebene und senkrechte zu Ihr. Wie werden diese Komponenten genannt?

B) bestimmen sie die Reibungskraft die zwischen kiste und Ebene wirkt und nennen sie die Gleitreibunsgzahl!

Problem/Ansatz:

Zu a) Die Zeichnung und Beschriftung entnehmt ihr dem Anhang. Was soll das heißen wie werden diese Komponenten genannt? Ist doch die Gewichtskraft die Reibungskraft und die Normalkraft oder?

Zu b) von der Reibungskraft wissen wir das diese F =-μ*N ist und N=m*a nun müsste man zunächst komponentenweise die Kraft Fg ausrechnen und als endergebnis müssten wir erhalten Fg+N+μ= 0,3m/s^2

Zu x = 9,8*sin(30)*15 = 73,5 N und zu y=9,8*cos(30)*15? 127,31

So bis hier hin bin ich jetzt gekommen. Hab ich jetzt mit y=127,31N=Fg und mit x=73,5N= Normalkraft ausgrechnet? Also irgendwas muss an der Formel noch verkehrt sein, da μ dimensionslos ist, ich aber noch m/s^2 habe. Und wegen der Gleitreibung. Ich verstehe den Unterschied nicht so ganz zwischen Reibung und Gleitreibung? Gibts da überhaupt einen? Und wenn ja wie unterscheiden sich diese und wie füge ich das in dieser Aufgabe ein?

Answer 1

Hallo MatheFee,

F_G = m · g  (g = Ortsfaktor 9,81 m/s²)

Komponenten von F_G: Normalkraft  F_N =  F_G · cos(30°)  =  m · g · cos(30°)

                                                                           [ senkrecht zur Ebene ]

                      Hangabtriebskraft:  F_H =  m · g · sin(30°)     [ parallel zur Ebene ]

Reibungskraft: F_R = μ · F_N =  μ · m · g · cos(30°) 

Gesamtkraft  F =  F_H - F_R =  m · a

                 F =  m · g · sin(30°)  - μ · m · g · cos(30°)  = m · a        m fällt raus

                         g · sin(30°)  - μ · g · cos(30°)  =  a

                           \(  μ  =  \dfrac{g·sin(30°)+0,3\frac{m} {s^2}} {g·cos(30°)}≈0,613\)

Für die Reibungskraft kannst du dann hier einsetzen.

Gruß Wolfgang

Answer 2

Hallo

richtig ist |Fr| =μ*N dass du N=m*a schreibst ist falsch was soll a sein? N=Fg*cos(30°)=mg*cos(30°)

völlig falsch ist dann dein Fg+N+μ= 0,3m/s  links steht ne Kraft rechts ne Beschleunigung. das +μ nahm ich mal als Tipfehler.

was nirgends steht ist die Hangabtriebskraft Fh=m*g*sin(30°) von der wird die Reibungskraft, die  gegen die Bewegungsrichtung wirkt abgezogen, dann hast du

m*a=m*g*sin(30°)-μ*mg*cos(30°) hier ist alles gegeben ausser μ, also kannst du das ausrechnen.

durch deine verschiedenen Bezeichnungen finde ich nicht durch, erst Kräfte dann x  das Newton sein soll, wahrscheinlich die Hangabtriebskraft? aber die ist nicht 9,8*sin(30)*15  sondern 9,8m/s^2*sin(30°)*15kg

dann schreibst du Fg für die Normalkraft und die Hangabtriebskraft = Normalkraft?

ziemliches Durcheinander.

also fang wie ich von vorne an

Gruß lul