Ich verzweifle an dieser Aufgabe.. Bitte helfe mir :)
Gerne - wenn ich nur genauer wüsste wie?
Die Aufgabe ist nicht wirklich genau gestellt. Und ja - eine Zeichnung ist absolut notwendig. Ich versuche mich mal:
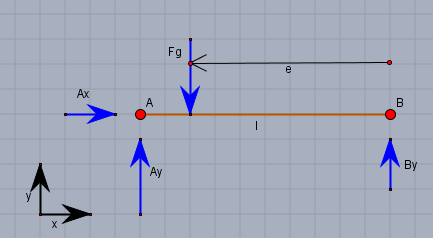
Ein Portalkran hat i.A. zwei Auflagestellen. Hier \(A\) und \(B\). Der Abstand der Auflager sei \(l\). Im Abstand von \(e\) vom Lager \(B\) greift eine nach unten gerichtete Kraft \(F_G\) an.
\(F_G\) sei gegeben und die Lagerkräfte sind gesucht. Der Vollständig halber wird \(A\) als Festlager angenommen. Daher existiert hier ggf. ein \(A_x\).
Wähle zunächst ein Koordinatensystem und rechne im Folgenden immer in positiver Richtung. D.h. Jedes Moment dreht gegen(!) den Uhrzeigersinn. Um die Kräfte zu berechnen, stellt man die Kräftesumme in X- und Y-Richtung und ggf. eine oder mehrere Momentensummen auf.
Kräfte in X: $$\sum F_x = 0 \implies A_x = 0$$
Kräfte in Y: $$\sum F_y = 0 \implies A_y + B_y - F_G = 0$$\(F_G\) wird negativ gerechnet, da \(F_G\) in negative Y-Richtung zeigt.
Momente um \(B\): $$-l \cdot A_y + e \cdot F_G = 0$$Das Moment aus \(A_y\) um \(B\) dreht im Uhrzeigersinn, daher ist das negativ. Aus der letzten Gleichung kann man bereits \(A_y\) berechnen:$$A_y = \frac el F_G$$Einsetzen in die Kräftesumme in Y liefert \(B_y\):$$B_y = F_G - A_y = F_G - \frac el F_G = \frac{l-e}{e} F_G$$Um zur ursprünglichen Frage zurück zu kommen: Verdoppelt sich \(F_G\) verdoppeln sich auch die Lagerkräfte (s. meine Antwort oben).
Falls mein Modell nicht zu Deiner Aufgabe passt, oder Du noch Fragen hast, so melde Dich bitte. Stelle möglichst konkrete Fragen.