Hallo,
Aber ich weiß leider nicht wo meine Höhe ist
Ok, aber Du hast das doch irgendwo abgezeichnet - oder? Ich gehe mal von \(4,5/2=2,25\) aus. Ich habe das zunächst zeichnerisch gelöst (ist irgendwie durchsichtiger!)
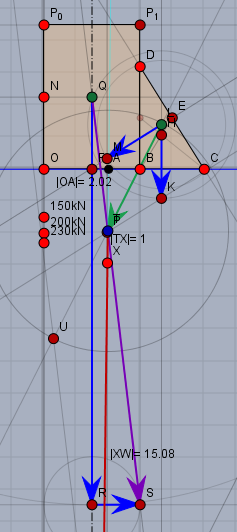
Leider doch unübersichtlich, weil die Kräfte so unterschiedlich groß sind - die Resultierende (rot) geht gar nicht auf's Bild. Das Ergebnis ist \(R=1608\,\text{kN}\) und die 'Aufstandsebene' wird bei \(x=2,02\) von der Resultierenden geschnitten, wenn man \(x=0\) am linken Rand des Rechtecks annimmt (Punkt \(O\)).
Nummerisch stellt man am Besten eine Tabelle auf:$$\begin{array}{rrrr|r}x& y& F_x& F_y& M_i\\ \hline 1,50& 0,00& 0,00& -1272,00& -1908,00\\ 0,00& 2,25& 150,00& 0,00& -337,50\\ 3,67& 0,00& 0,00& -230,00& -843,33\\ 4,00& 1,60& -169,60& -106,00& -152,64\\ \hline a& 0& -19,60& -1608,00& -3241,47\end{array}$$Die ersten beiden Spalten sind die Angriffspunkte in einem Koordinatensystem, wo die X-Achse nach rechts und die Y-Achse nach oben zeigt. Den Ursprung habe ich ín den Punkt \(O\) gesetzt. Bei Kräften, die horizontal bzw. vertikal verlaufen ist natürlich die Y- bzw. X-Koordinate irrelevant. man kann den 'Angriffspunkt' überall auf der Kraftlinie setzen.
Die Momente um den Ursprung \(O\) berechnen sich jeweils aus$$M_i = x \cdot F_y - y \cdot F_x$$
Die resultierende Kraft \(R\) ist $$R = \sqrt{ (-19,6)^2 + (-1608)^2} \,\text{kN}\approx 1608,12 \,\text{kN}$$Und die X-Koordinate \(a\) des Schnittpunktpunkts der Wirklinie von \(R\) mit 'Aufstandsebene' (\(y=0\)) berechnet sich aus:$$ a \cdot R_y = M_{\text{ges}} \implies a \approx 2,02$$ (s. letzte Zeile in der Tabelle)
Falls Du noch Fragen hast, so melde Dich bitte.
Ich schreibe morgen eine Arbeit.
melde Dich das nächste Mal einfach früher. Auch Leute, die hier antworten, brauchen etwas Zeit und sind nicht immer online ;-)
Gruß Werner