Hallo Windhund,
"Das müsste ja die b.) sein," Nein - das wäre das \(s\)-\(t\)-Diagramm , wenn die Geschwindigkeit des Zuges konstant wäre. Schaue auf folgende Skizze
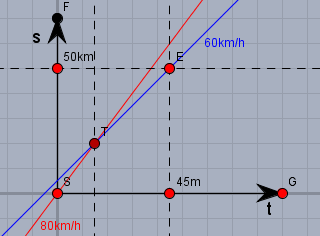
Die rote Gerade zeigt den Verlauf eines Zuges, der sich mit 80km/h bewegt und die blaue den Verlauf, wenn er sich mit 60km/h bewegt. Wenn ich mal annehme, dass der Zug mit 80km/h startet und mit 60km/h ankommt, so geht der Verlauf von \(S\) über \(T\) nach \(E\).
"Wie groß sind die Teilstrecken und die Fahrzeit für die erste Teilstrecke?"
\(t_1\) sei die Zeit, zu der der Zug die Geschwindigkeit reduziert. Für das erste Stück gilt dann
$$s(t) = 80 \text{km/h} \cdot t$$ und für das Stück zwischen dem Punkt \(T\) und \(E\)
$$s(t) = 60 \text{km/h} \cdot (t - 45\text{min}) + 50\text{km}$$
Im Punkt \(T\) zum Zeitpunkt \(t_1\) gelten beide Verläufe - also ist
$$80 \text{km/h} \cdot t_1 = 60 \text{km/h} \cdot (t_1 - 45\text{min}) + 50\text{km}$$ $$\begin{aligned} 20 \text{km/h} \cdot t_1 &= -60 \text{km/h} \cdot 45\text{min} + 50\text{km} \\ &= -60 \text{km/h} \cdot \frac34 \text{h} + 50\text{km} \\&= -45 \text{km} + 50\text{km} = 5\text{km} \end{aligned}$$ $$\space \Rightarrow t_1 = \frac14 \text{h} = 15 \text{min}$$
Das ersten (schnelle) Teilstück \(s_1\) ist $$s_1 = s(t=\frac14 \text{h}) =80 \text{km/h} \cdot \frac14 \text{h} = 20 \text{km}$$ Gruß Werner