Hier nun die Lösung (wird etws länger werden) =):
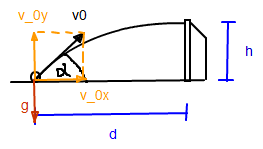
Geschwindigkeitskomponenten $$v_{0_y}=v_0\,sin\alpha$$ und $$v_x=v_0\,cos\alpha$$
Bewegungsgleichung (auf ausführliche Integration wird hierbei verzichtet, das würde den Rahmen sprengen):
in y-Richtung:
$$a_y=-g$$ $$v_y=-g\,(t-t_0)+v_{0_y}$$ $$y(t)=y=-\frac{1}{2}g(t-t_0)^2+v_{0_y}(t-t_0)+y_0\,\,\,\,\,\,\,\,Gl.(1) $$
in x-Richtung:
$$a_x=0$$ $$v_x=v_{0_x}$$ $$x(t)=x=v_{0_x}(t-t_0)+x_0\,\,\,\,\,\,\,\,Gl.(2) $$
$$Gl.2$$ nach $$(t-t_0) = \frac{x-x_0}{v_{0_x}}$$ aufgelöst und in $$Gl.1$$ eingesetzt:
$$a_y=-g$$ $$v_y=-g\,(t-t_0)+v_{0_y}$$ $$y(x)=y=-\frac{1}{2}g\left( \frac{x-x_0}{v_{0_x}}\right)^2+v_{0_y}\left( \frac{x-x_0}{v_{0_x}}\right)+y_0\,\,\,\,\,\,\,\,Gl.(1) $$
Mit den Geschwindigkeitskomponenten ergibt sich folgende Gleichung:
$$a_y=-g$$ $$v_y=-g\,(t-t_0)+v_{0_y}$$ $$y(x)=y=-\frac{1}{2}g\left( \frac{x-x_0}{v_0\,cos\alpha}\right)^2+v_0\,sin\alpha\left( \frac{x-x_0}{v_0\,cos\alpha}\right)+y_0\,\,\,\,\,\,\,\,Gl.(1) $$
$$y(x)=y=-\frac{1}{2}g \frac{(x-x_0)^2}{v^2_0\,cos^2\alpha}+\frac{v_0}{v_0}\, \frac{sin\alpha}{cos\alpha}(x-x_0)+y_0\,\,\,\,\,\,\,\,Gl.(1) $$
$$y(x)=y=-\frac{1}{2}g \frac{(x-x_0)^2}{v^2_0\,cos^2\alpha}+tan\,\alpha(x-x_0)+y_0\,\,\,\,\,\,\,\,Gl.(1) $$
auf folgenden Beweis wird verzichtet:
$$\frac{1}{cos^2\alpha}=1+tan^2\,\alpha$$
$$y(x)=y=-\frac{g}{2\,v^2_0}\,(1+tan^2 \alpha) (x-x_0)^2+tan \alpha (x-x_0)+y_0$$
Bedingungen: $$y_0=0,\,\,x_0=0,\,\,y(x=d)=h$$
$$y(x=d)=-\frac{g}{2\,v^2_0}\,(1+tan^2 \alpha) \, \cdot \, d^2+tan \alpha\, \cdot \, d = h$$
$$h=-\frac{g}{2\,v^2_0}\,(1+tan^2 \alpha) \, \cdot \, d^2+tan \alpha\, \cdot \, d$$
Daraus erhält man eine quadratische Gleichung:
$$0=-\frac{g}{2\,v^2_0}\,(1+tan^2 \alpha) \, \cdot \, d^2+tan \alpha\, \cdot \, d\,-h$$
Substitution mit $$z\,=\,tan\,\alpha$$
$$\frac{g \cdot d^2}{2\,v^2_0} \cdot z^2 - d \cdot z + \frac{g \cdot d^2}{2\,v^2_0} + h = 0$$
$$z_{1/2} = \frac{v^2_0}{g\,d} \cdot \left(1 \pm \sqrt{1-\frac{2\,g}{v^2_0} \cdot \left(h + \frac{g\,d^2}{2\,v^2_0}\right)}\right)$$
$$\alpha_1 = arctan\,z_1$$
$$\alpha_2 = arctan\,z_2$$