Freier Fall. s-t-Diagramm. Zurückkehrender Schall. Münze fällt in Brunnen.

Question

Ein stein wird in einen tiefen brunnen fallen gelassen. Man hört ihn nach 6 Sekunden aufschlagen. Zeichnen Sie ein s-t-Diagramm des fallenden Steins und des zurückkehrenden Schalls (340 m/s).

Welche Tiefe ergiebt sich aus dem Diagramm? Rechnen Sie nach?

Was genau ist mit dem zurückkehrenden Schall gemeint?

Wie zeige ich das am Diagramm? ich doch gar keine Werte für t...

Welche Formeln brauche ich,....

 

Danke im Voraus :)

Comments

??? Schläfst du etwa schon?

Answer 1

Vom Zeitpunkt des loslassen bis zum hören des schalls vergehen 6s, die geschwindigkeit des schalls wird hier mit 340m/s angegeben. folglich  gilt für  die Strecke

f(x) = x *340 m/s        x=zeit=t     oder auch f(t) = t*340

x=6s     f(x) =6*340m/s=2040m

 

 

Comments

Ich denke Du hast etwas vergessen.

Answer 2

Freier Fall:
x = 1/2 * g * t^2  // g=Ortsfaktor, x=Tiefe des Brunnens
--> t_FreierFall = sqrt(2x/g)  // nur positive Lösung sinnvoll

Schallgeschwindigkeit:
x = v_Schall * t  // v_Schall =Schallgeschwindigkeit, x=Tiefe des Brunnens
t_Schall = x / v_Schall

Eräuterung des Ablaufs:
Der Stein wird losgelassen, in Folge der Erdanziehung nach unten mit g beschleunigt. Die Zeit, die der Stein für den Weg nach unten braucht ist t_FreierFall. Beim Aufprall auf den Brunnengrund erzeugt der Stein ein Geräusch; dieser Schallimpuls bewegt sich mit Schallgeschwindigkeit nach oben und ist nach t_Schall zu hören. t_gesamt=6s ist daher:
t_gesamt=t_FreierFall+t_Schall

Einsetzen ergibt:
t_gesamt= t_FreierFall+ x / v_Schall

Umstellen:
t_FreierFall = t_gesamt- x / v_Schall

in x = 1/2 * g * t^2 liefert:
x^2 -x*(2v_Schall/g + 2v_schallt_gesamt) + t_gesamt^2 * v_Schall^2 = 0

mit Lösungsformel für Qudratische Gleichungen:

x₁= 151,35 m
x₂= 27496,44 m

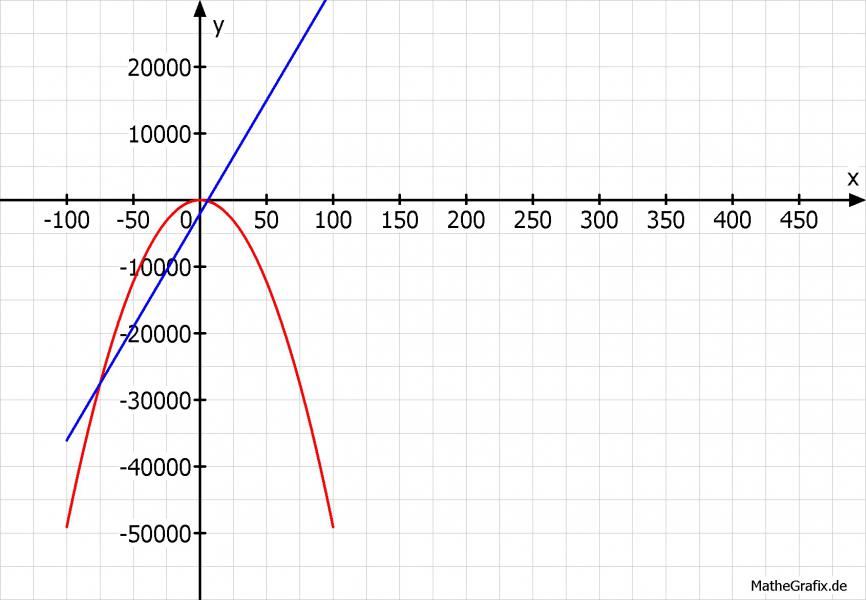
Auf Bild eins sieht man, dass die Gerade die Parabel zweimal schneidet, der Schnittpunkt bei x₂ liegt aber im negativen Zeitbereich, also bei einem Zeitpunkt der vor dem Loslassen des Steins liegt, und ist deshalb auch keine sinnvolle Lösung.

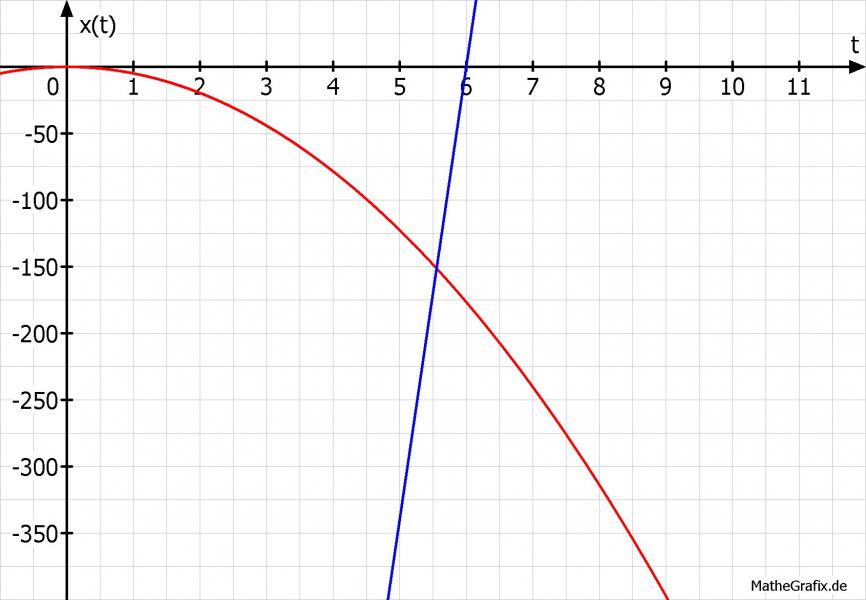
Verwendete Parabelgleichung: x(t) = -1/2 * g * t^2   Verwendete Geradengleichung: x(t) = v_s * (t - 6s)

Die Parabel beschreibt den Fall des Steines in Abhängigkeit von der Zeit. Durch die Erdanziehungskraft beschleunigt er während seines Falls, das heißt seine Geschwindigkeit nimmt immer mehr zu. Der Schall hingegen bewegt sich mit konstanter Geschwindigkeit, daher die Gerade. Der Stein beginnt seine Bewegung bei t=0 und x=0, daher liegt der Scheitelpunkt der Parabel auch im Ursprung. Der Schall kommt zum Zeitpunkt t=6 bei x=0 Null an, deshalb ist die Gerade auch um 6s nach rechts verschoben. Die Steigung entspricht der Schallgeschwindigkeit. Der Schnittpunkt im positiven Zeitbereich entspricht der Tiefe des Brunnens.

Bei Fragen --> Kommentar.