Ich musste mich zunächst kundig machen.
a.)
Zunahme der potentiellen Energie
E ( pot ) = m2 * g * h = 1000 kg * 9.81 m/s^2 * 900*10^3 m
E ( pot ) = 8.829 * 10^9
b.)
An der Erdoberfläche
r = Erdradius 6371 km
F = G * m1 * m2 / r^2
F = G * m1 * m2 / ( 6371 * 10^3 )^2 = 1000 * 9.81
G * m1 * m2 = 3.982 * 10^17
F ( r ) = 3.982 * 10^17 / r^2
Probe
F ( 6371*10^3) = 3.982 * 10^17 / (6371*10^3 )^2
F ( 6371*10^3) = 9810 N
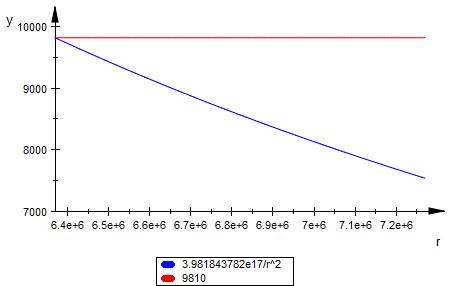
x-Achse 6371 km bis ( 6371 + 900 ) km
blaue Kurve : abfallendes Gewicht des Satelitten
rote Kurve : konstantes Gewicht
Die Arbeit bei rot ist das Rechteck unterhalb von rot
9810 * 900 * 10^3
8,829 * 10^9
Der Arbeit bei blau ist
∫ 3.982 * 10^17 / r^2 dr zwischen 6371 *10^3 bis 7271 * 10^3
[ -3.982 * 10^17 / r ] ...
7.736 * 10^9
So weit so gut ?