 Aufgabe:
Aufgabe:
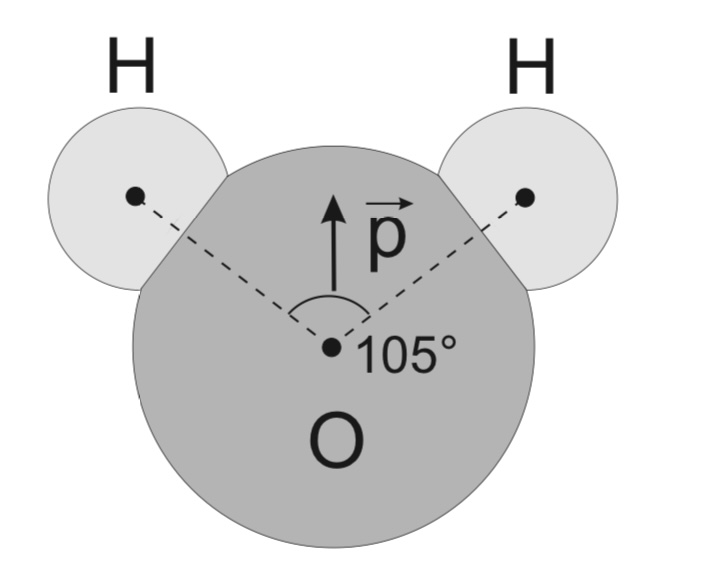
1. Wassermolekül als elektrischer Dipol
Ein neutrales Wassermolekül besitzt ein elektrisches Dipolmoment \( p=6,2 \cdot 10^{-30} \mathrm{C} \cdot \mathrm{m} \). Die Elektronen des Moleküls halten sich näher beim Sauerstoffkern als bei den Wasserstoffkernen auf, wodurch die 'Sauerstoffseite' des Moleküls stärker negativ geladen ist als die 'Wasserstoffseite'. Das elektrische Diplomoment \( \vec{p} \) ist daher parallel zur Symmetrieachse des Moleküls zur 'Wasserstoffseite' hin gerichtet.
a) Das Dipolmoment \( p \) wird durch den Betrag \( q \) der getrennten, positiven und negativen Ladungen sowie den Abstand \( d \) zwischen ihren Schwerpunkten bestimmt. Berechnen Sie \( d \) unter der Annahme, dass 8 Elektronen (und entsprechend 8 positive Ladungen) am Diplomoment beteiligt sind und vergleichen Sie das Resultat mit der Bindungslänge \( a_{O H}=96 \mathrm{pm} \) zwischen dem O- und einem H-Atom im Molekül!
b) Bestimmen Sie das maximale Drehmoment in einem homogenen elektrischen Feld mit der Feldstärke \( E=1,5 \cdot 10^{4} \mathrm{~V} / \mathrm{m} \) !
c) Leiten Sie einen Ausdruck für die Arbeit \( W_{a} \) her, die aufzubringen ist, um das Molekül im elektrischen Feld aus seiner vollständig ausgerichteten Position heraus \( \left(\vec{p} \| \vec{E}\right. \) ) um \( 180^{\circ} \) zu drehen!
Berechnen Sie anschließend \( W_{a} \) für die im Text genannten Zahlenwerte!
Ich habe einmal die ganze Aufgabe gepostet, damit man es nachvollziehen kann und zwar habe ich und a und b gelöst aber bei c) komme ich nicht weiter , wie komme ich auf die Formel um die Arbeit auszurechnen?