Hallo, ich habe folgende Aufgabe. Ich muss die im Phasendiagramm des harmonischen Oszillators (siehe Bild) von der Ellipse umschlossene Fläche durch die Erhaltungsgröße \( E \) und die Frequenz \( \omega=\sqrt{k / m} \) ausdrücken.
Weiß jemand, wie man das macht?
Ich bedanke mich im Voraus für eure Hilfe!
Text erkannt:
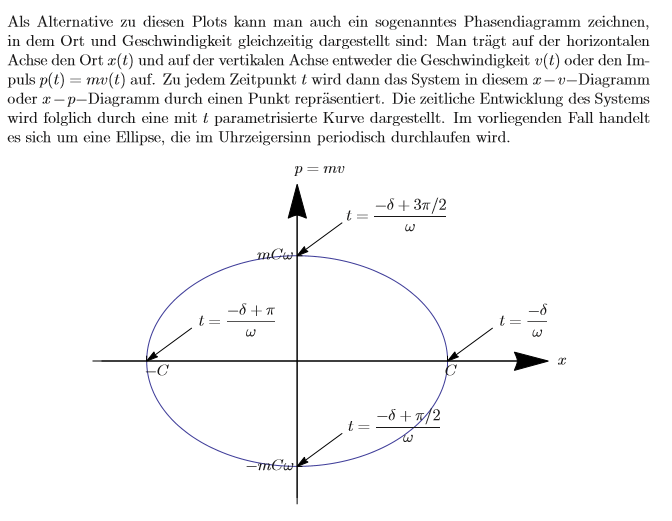
Als Alternative zu diesen Plots kann man auch ein sogenanntes Phasendiagramm zeichnen,
in dem Ort und Geschwindigkeit gleichzeitig dargestellt sind: Man trägt auf der horizontalen
Achse den Ort \( x(t) \) und auf der vertikalen Achse entweder die Geschwindigkeit \( v(t) \) oder den Im-
puls \( p(t)=m v(t) \) auf. Zu jedem Zeitpunkt \( t \) wird dann das System in diesem \( x-v- \) Diagramm
oder \( x-p- \) Diagramm durch einen Punkt repräsentiert. Die zeitliche Entwicklung des Systems
wird folglich durch eine mit \( t \) parametrisierte Kurve dargestellt. Im vorliegenden Fall handelt
es sich um eine Ellipse, die im Uhrzeigersinn periodisch durchlaufen wird.
$$ -m G_{\omega} $$