Hydrostatische Auftriebskraft - Kräftegleichgewicht

Question

Aufgabe:

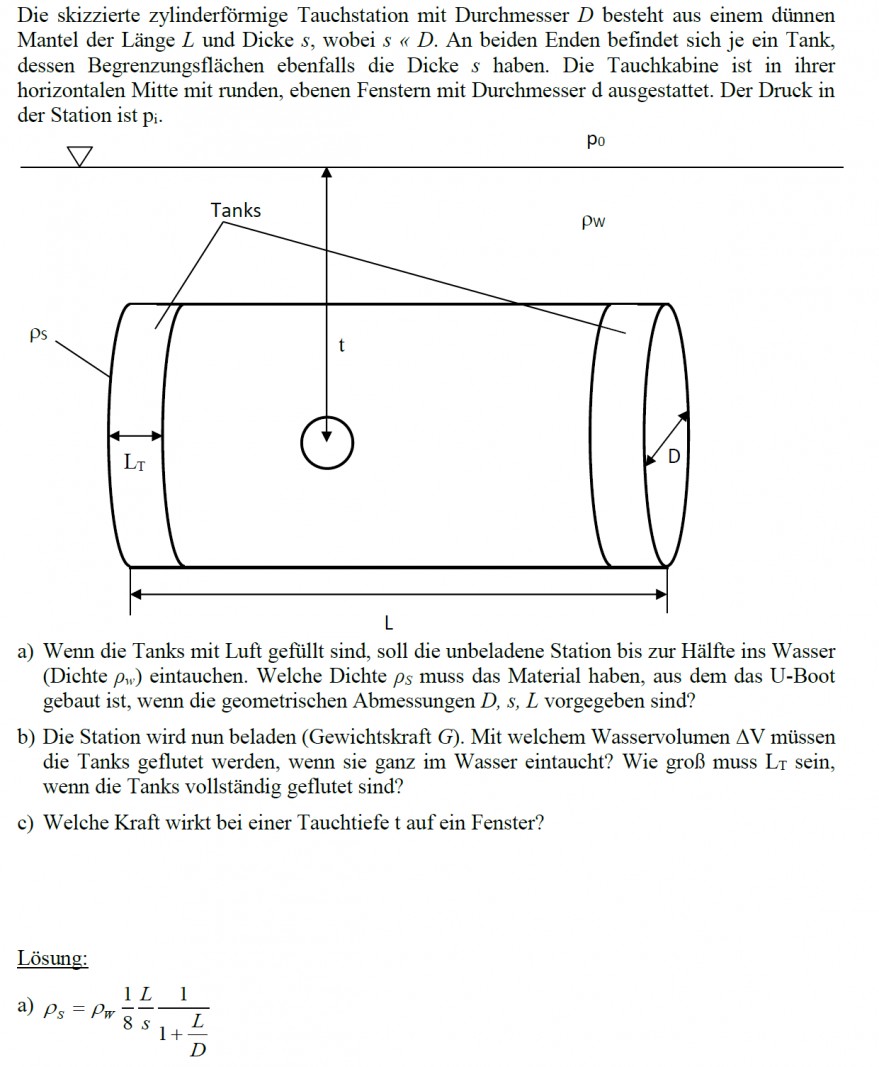
Text erkannt:

Die skizzierte zylinderförmige Tauchstation mit Durchmesser \( D \) besteht aus einem dünnen Mantel der Länge \( L \) und Dicke \( s \), wobei \( s \) " \( D \). An beiden Enden befindet sich je ein Tank, dessen Begrenzungsflächen ebenfalls die Dicke \( s \) haben. Die Tauchkabine ist in ihrer horizontalen Mitte mit runden, ebenen Fenstern mit Durchmesser d ausgestattet. Der Druck in der Station ist pi.

a) Wenn die Tanks mit Luft gefüllt sind, soll die unbeladene Station bis zur Hälfte ins Wasser (Dichte \( \rho_{w} \) ) eintauchen. Welche Dichte \( \rho_{S} \) muss das Material haben, aus dem das U-Boot gebaut ist, wenn die geometrischen Abmessungen \( D, s, L \) vorgegeben sind?

Lösung:
a) \( \rho_{S}=\rho_{W} \frac{1}{8} \frac{L}{s} \frac{1}{1+\frac{L}{D}} \)

Problem/Ansatz:

Der Ansatz wird eine einfache Kräftebilanz für die Station sein. Meine Überlegung ist, dass die Gewichtskraft wirkt und die hydrostatische Auftriebskraft nach Archimedes. Da die Tauchstation zur Hälfte eingetaucht, ist das verdrängte Flüssigkeitsvolumen die Hälfte des Volumens der Tauchstation und ich komme damit zu dem Ergebnis ρ_s = 0.5*ρ_w.

Die Lösung habe ich auch mit angegeben. Mir fehlt jedoch noch der Ansatz, wie ich darauf komme. Ich würde mich über einen Tipp freuen!

Answer 1

Hallo

du willst ja die dichte des Wandmaterials, das ist sicher nicht 1/2ρW

also musst du erst das Volumen des Materials berechnen: dazu die Oberfläche des Zylinders *s + die 2 inneren Scheiben mit Fläche*s ( dass man einfach O*s rechen darf liegt an s<<D)

aus dem halben Volumen des Zylinders hast du die Masse des verdrängten Wassers  und setzest sie gleich mit Volumen mal Dichte des Wandmaterials.

Gruß lul