Länge im gleichseitigen Dreieck?

Question

Aufgabe: Wie kommt man auf die Länge b=a/√3

Problem/Ansatz: Hallo, gefragt ist in Aufgabe 4 Die Länge b=a/√3. Wie kommt man darauf??? Auf a bin ich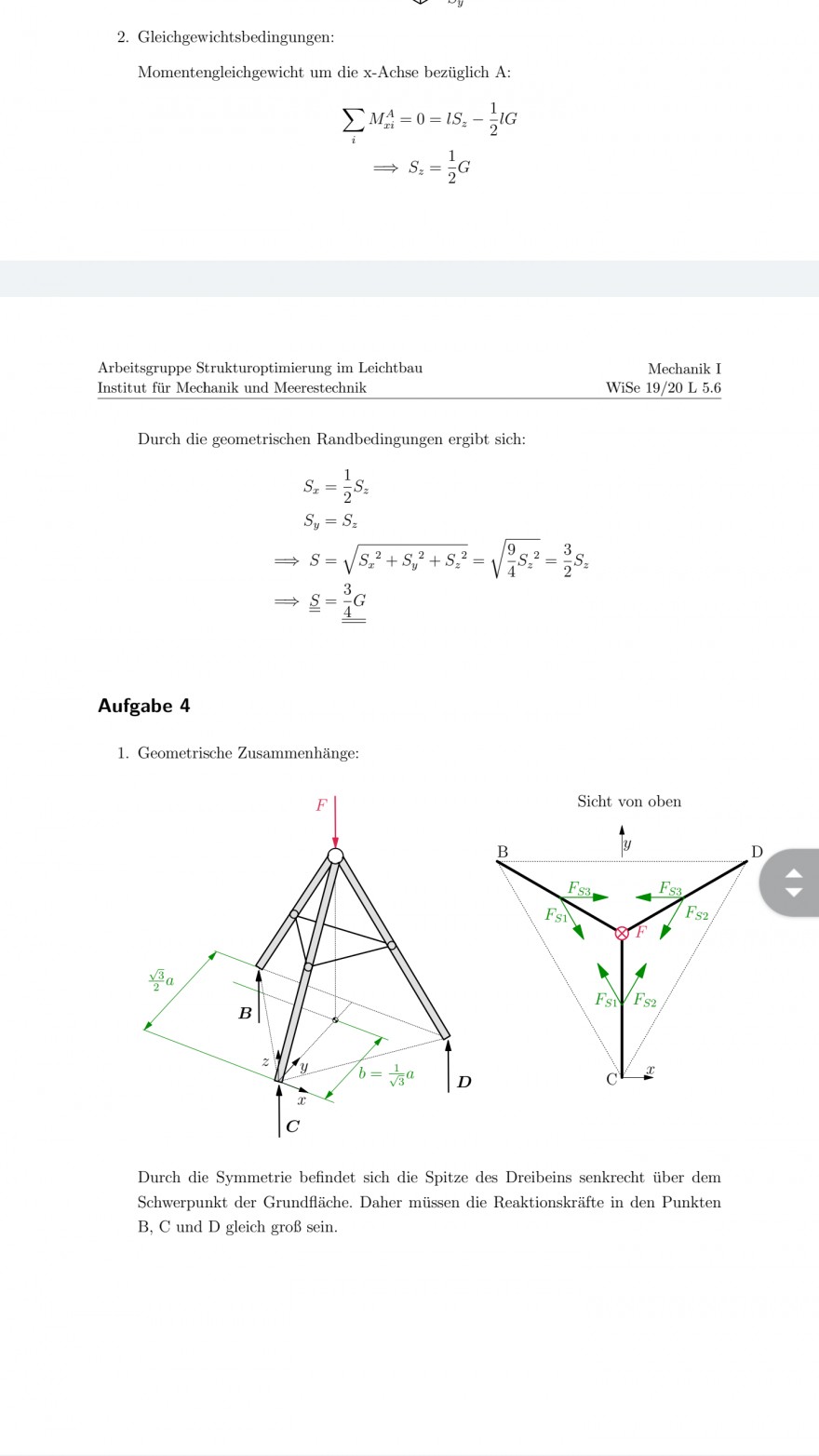

Text erkannt:

Gleichgewichtsbedingungen:
Momentengleichgewich um die x-Achse beziglich A:
$$ \sum \limits_{i} M_{i j}^{M}=0=I S_{i}-\frac{1}{2} C $$
\( \Rightarrow S_{z}= \)
ngungen ergibt
\( +S_{z}^{2}=\sqrt{4} \)
Aufgabe
170

 

Text erkannt:

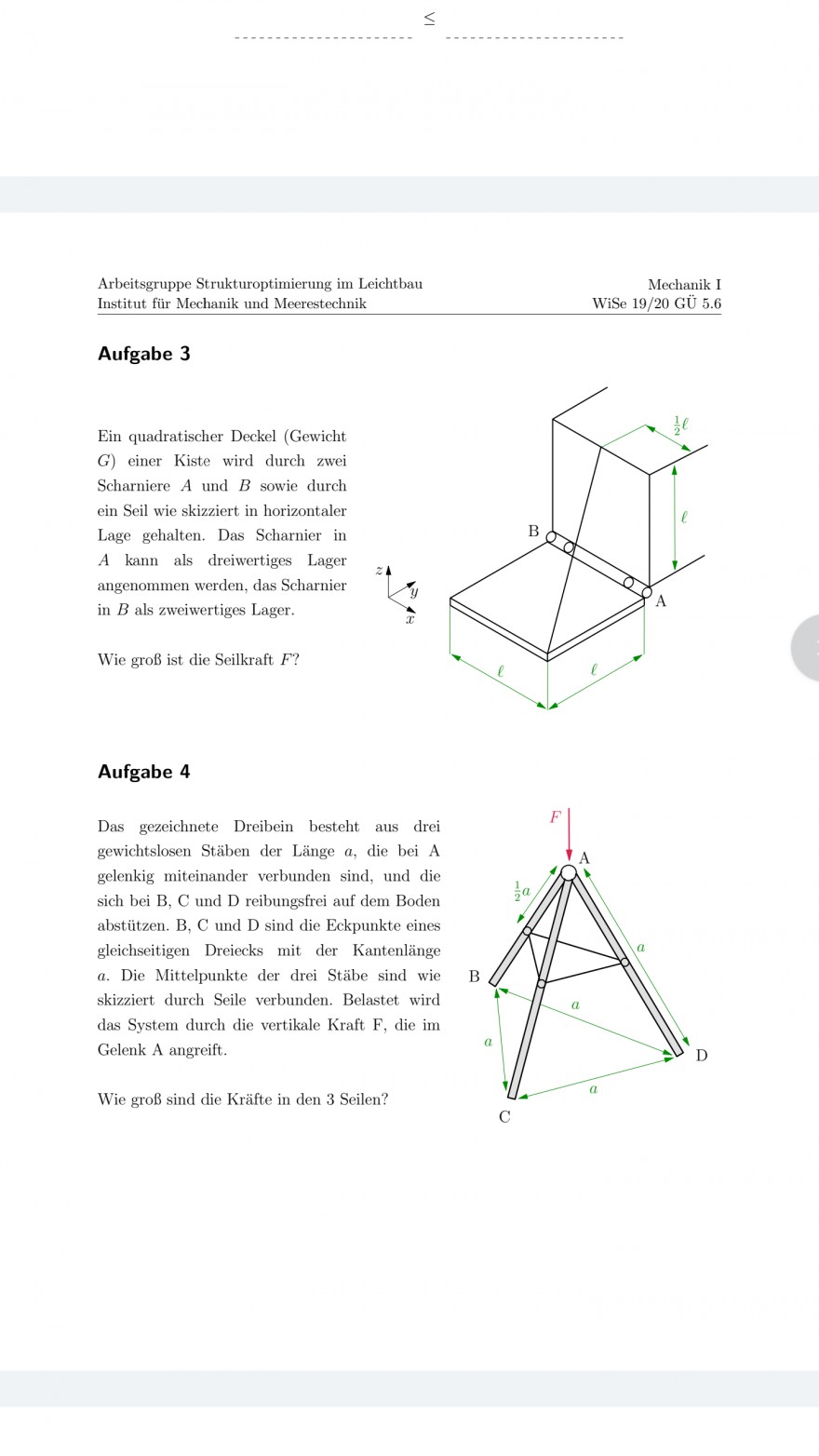
Aufgabe 3
Aufga
Das geeeichnete Dreibein besteht
11
abetivatific tigests mit dis the situe wire \( B \) a Die niterh sid seturidel Kreater form in divisiet divent did sessuncie Kreft F, die in

bereits mit dem Satz des Phytagoras gekommen....

Answer 1

Hallo Kamjam,

Wie kommt man auf die Länge b=a/√3

Die Standfläche des Dreibeins ist ein gleichseitiges Dreieck mit der Seitenlänge \(a\). Die Höhe im gleichseitigen Dreieck ist (nach Pythagoras) \(h= \frac 12 \sqrt 3 \, a\) (s. Bild bei Aufgabe 4).

Im gleichseitigen Deieck fallen Höhen und Seitenhalbierende zusammen und somit auch der Schwerpunkt (Schnittpunkt der Seitenhalbierenden) und der Höhenschnittpunkt. Und da sich die Seitenhalbierenden immer im Verhältnis \(2 \div 1\) schneiden, Ist die Strecke \(b\) von einer Ecke des Dreiecks zum Schwerpunkt hier $$b = \frac 23 h = \frac 23 \cdot \frac 12 \sqrt 3 \, a = \frac 1{\sqrt 3} a$$

Comments

Hallo Werner,

wenn ich es ausmultipliziere, komme ich auf (2/6)√3a

Gekürzt ist es dann: (1/3)√3a, also √3a/3 ???

---

Ahhh oder du hast dann mit √3 erweitert. Ok dankee :)

---

Ahhh oder du hast dann mit √3 erweitert. Ok dankee :)

genau genommen wurde durch \(\sqrt 3\) gekürzt:$$  \frac 23 \cdot \frac 12 \sqrt 3 \, a = \frac {\sqrt 3}3  \, a =\frac {\cancel{\sqrt 3}}{\sqrt 3 \cancel{\sqrt 3}} \, a = \frac{a}{\sqrt 3}$$wobei ich persönlich es nicht so machen würde! Ich würde den Ausdruck \(\frac 13 \sqrt 3\, a\) so stehen lassen.

Ausdrück mit Wurzeln sollten, genau wie Ausdrücke mit negativem Vorzeichen oder imaginären Anteilen, nicht im Nenner eines Bruches stehen. Das macht Ergebnisse dann vergleichbarer.

Aber anscheinend wird diese Vorgehensweise ncht mehr gelehrt.