Bergsteiger am Seil (Kräftegleichgewicht)

Question

Aufgabe:

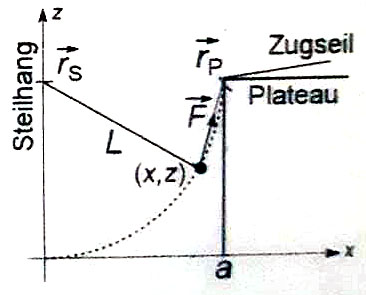
Ein Bergsteiger (Masse m) hängt wie skizziert im Seil der Länge L, welches bei r_S am Steilhang befestigt ist. Er wird nun reibungsfrei mit einem weiteren Seil herüber auf ein bei r_P beginnendes Plateau in der gleichen Höhe wie die Steilhangbefestigung gezogen und durchläuft dabei die Punkte (x,z).
(a) Formulieren Sie im gegebenen Koordinatensystem das statische Kräftegleichgewicht. Zeigen Sie hiermit, dass für die Kraft F(x) in Abhängigkeit von der Koordinate x gilt:

$$F(x) = mg*\frac{x}{a}*\frac{\sqrt{(a-x)^2 + L^2-x^2}}{\sqrt{L^2-x^2}} $$

Problem:

Ich würde gerne wissen, wie man auf diese Formel kommt.

Mir ist klar, dass die Terme unter der Wurzel vom Pythagoras kommen:

Der Wurzelterm über dem Bruchstrich ist die Länge der Strecke, wo F dransteht.

Und der Term im Nenner ist die senkrechte Höhe des Bergsteigers zum Plateau.

Aber wie kommt man auf diese Formel?

Man hat einmal die senkrechte Kraft nach unten F_G = mg.
Als Gegenkräfte hat man eine entlang von L und eine entlang von F.

Comments

Ich komme nicht recht voran.

Meine Idee war noch, mit dem Sinussatz zu arbeiten, aber damit komme ich bis jetzt auch nicht auf die Formel.

Hat irgendjemand eine Idee?

Answer 1

Hallo Willy,

Die \(z\)-Koordinate in Abhängigkeit von \(x\) ist doch$$z=L -\sqrt{L^2 - x^2}$$(Kreisgleichung negiert plus \(L\)). Die Richtung der Kräfte \(\vec{F}\) und \(\vec{S}\), die im rechten Seil, sind durch die Aufhängepunkte gegeben$$\vec{F} = k_F \cdot \left(  \begin{pmatrix} a\\L \end{pmatrix} - \begin{pmatrix} x\\L -\sqrt{L^2 - x^2} \end{pmatrix} \right) \\ \space = k_F \cdot \begin{pmatrix} a-x\\\sqrt{L^2 - x^2} \end{pmatrix} \\ \vec{S} = k_S \cdot \left( \begin{pmatrix} 0\\L \end{pmatrix} - \begin{pmatrix} x\\L -\sqrt{L^2 - x^2} \end{pmatrix}\right) \\ \space = k_S \cdot \begin{pmatrix} -x\\\sqrt{L^2 - x^2} \end{pmatrix}$$Wobei \(k_F\) und \(k_S\) noch unbekannte Größen sind. Es muss weiter gelten$$\vec{F} + \vec{S} + \vec{C} = 0 \quad \text{ mit }\space \vec{C} = \begin{pmatrix} 0 \\ -mg \end{pmatrix}$$

Alle Kräfte einsetzen gibt$$k_F \cdot \begin{pmatrix} a-x\\\sqrt{L^2 - x^2} \end{pmatrix} + k_S \cdot \begin{pmatrix} -x\\ \sqrt{L^2 - x^2} \end{pmatrix} + \begin{pmatrix} 0 \\ -mg \end{pmatrix} = 0 \\ k_F a - (k_F+k_S) x = 0 \implies k_F +k_S = \frac{k_F a}{x}\\ (k_F+k_S) \sqrt{L^2 - x^2} - mg = 0$$

Das \(k_F+k_S\) in die zweite Gleichung einsetzen:$$\begin{aligned} \frac{k_F a}x \sqrt{L^2-x^2} - mg&= 0 \\ k_F a \sqrt{L^2-x^2} &= xmg \\ k_F &= \frac{xmg}{a \sqrt{L^2-x^2}} \end{aligned}$$und jetzt den Wert für \(k_F\) in \(\vec F = k_F \cdot \dots\) einsetzen$$\vec F = \frac{xmg}{a \sqrt{L^2-x^2}} \begin{pmatrix}a-x \\\sqrt{L^2- x^2}\end{pmatrix} $$Und der Betrag \(|\vec F| = F = \sqrt{\vec F^2}\) ist$$F =\frac{xmg}{a \sqrt{L^2-x^2}} \sqrt{ (a-x)^2+ L^2-x^2}$$siehe Formel oben.

Gruß Werner

Comments

Interessante Lösung.

Vielen Dank!