Wann kommt Auto zum Stehen?

Question

Aufgabe:

Hallo, wer kann helfen?

Es geht um ein Spielzeugauto, welches mit a = 8,0 cm/s^2 eine Rampe runter rollt. Unten angekommen auf einer Horizontale beträgt der Rollreibungskoeffizient 0,01 bis das Auto zum Stehen kommt. Es soll ein s(t) und v(t) - Diagramm gezeichnet werden mit den benötigten Größen.

Problem/Ansatz:

Ich bin über die Formel für die Rollreibung und F=m*g auf eine negative Beschleunigung auf der Horizontale von -9,81 cm/s^2 gekommen. Ich weiß allerdings nicht, nach welcher Zeit die Höchstgeschwindigkeit erreicht wird und wann das Auto zum Stehen kommt und wie hoch die Höchstgeschwindigkeit am Ende der Rampe ist

Answer 1

Hallo
es fehlt die Länge der Rampe! und die Masse des Autos. wenn dein a richtig ist ist es 10g?
wenn du die hast, dann ist s=a/2*t^2  daraus t, dann ve=a*t , s=Länge der Rampe dann bis zum Stillstand s=ve*t+-9,81cm/s^2/2*t^2 und 0=ve-9,81cm/s^2*t
Gruß lul

Comments

Hallo, mein s(t) - Diagramm ist leider falsch, ich soll es mir nochmal überlegen. Das Stück auf der Rampe soll richtig sein, habe das mit s=a/2*t^2 im Diagramm dargestellt und ähnelt einer Parabel. Aber auf der Horizontale, wo das Auto durch die Rollreibung langsam bremst, muss ich dann auch diese Formel anwenden? Wie sieht dieses Stück im s(t)-Diagramm aus? Geht die Kurve auch nach oben wie eine Parabel oder muss man die Kurve umdrehen, weil es sich ja um eine Bremsbeschleunigung handelt? Der Graph sähe dann so aus wie eine Wurzelfunktion. Wer könnte mir das s(t)-Diagramm skizzieren? Vielen Dank! Gruß Tino

---

nein keine Wurzelfunktion . Da steht doch s(t)=ve*t-a/2t^2 das ist eine nach unten geöffnete Parabel, wenn der Weg bei t=0 anfängt . du hast noch immer nicht gesagt, wie lange die Rampe ist, oder welche Zeit das A uf der Rampe fährt. Wenn du genaue Hilfe willst musst du immer die ganze Aufgabe schreiben.

---

Hallo, die Aufgabe lautet so: Ein Spielzeugauto rollt mit einer Beschleunigung von 8 cm/s^2 eine Rampe hinunter. Auf der anschließenden Horizontale bleibt es bei einer Rollreibung von 0,01 nach 12 s stehen. Mehr Daten sind nicht gegeben. Könnten Sie mir bitte das s(t)-Diagramm skizzieren bis zum Stillstand des Autos?

---

 ist die Masse des Autos 10 g ? oder wie kommst du auf a=9,81cm/s?

wenn dieses a stimmt, dann ist die Anfangsgeschwindigkeit va auf der e ebenen Strecke  mit  va-9,81cm/s^2*12s =0 ; va=117,72cm/s

dann ist die zeit auf der Rampe durch v=117cm/s=8cm/s^2*t also t=14,7s.

 also ist der erste Teil, von 0 bis 14,7s s(t)=4cm/s^2*t^2 also eine nach oben geöffnete Parabel, die bei 864cm endet

für die Zeit danach hat man s(t)=864cm+117cm/s*(t-14,7s)-9,81/2*(t-14,7s)^2

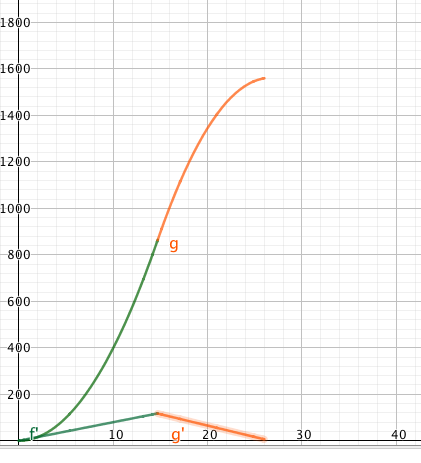
ich hab das mal platten lassen grün auf der Rampe, orange in der Ebene, unten die Geschwindigkeiten,

x-Achse in s, y Achse in cm.

---

Hallo und vielen Dank! Ich bin auf den Graph s(t) einfach nicht gekommen, besonders der orange Zweig auf der Ebene.

Die Masse des Autos hat sich ja bei mir aufgehoben. Ich hatte das doch von hinten her berechnet. Ich habe die Kraft berechnet, mit welcher das Auto beschleunigt wird (Produkt aus der Rollreibung μ*m*g, also 0,01*m*g. Dann mit der Gleichung F=m*a. Die 2 Kräfte habe ich gleichgesetzt, ergibt die Gleichung

m*a=μ*m*g also a=μ*g also 0,01*9,81m/s^2

Das hat unser Lehrer als richtig befunden. Über die Formel v=a*t bin ich dann auf v=117,72 cm/s gekommen, die Geschwindigkeit am Beginn der Ebene, soll auch so richtig sein