Hallo liebe Leute,
ich verstehe bei dieser Aufgabe die Lösung nicht.
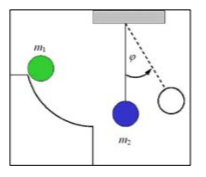
Erhaltungssätze: Eine homogene Kugel der Masse m1=0,3kg und
Radius 1
r = 0,2m rollt eine Bahn in Form eines Viertelkreises mit dem
Radius R =1m herunter und stößt mit einer zweiten Kugel mit gleichem
Radius und der Masse m2=0,2kg zentral und elastisch zusammen. Die
zweite Kugel hängt an einem L=1,2m langen Seil. Die Masse des Seils
ist vernachlässigbar.
Aufgabe a und b konnte ich lösen und verstehe ich auch.
Nur bei Aufgabe c) die Lösung verstehe ich nicht.
$$u _ { 2 } = \frac { 2 m _ { 1 } } { m _ { 1 } + m _ { 2 } } \cdot v _ { 1 } + \frac { m _ { 2 } - m _ { 1 } } { m _ { 1 } + m _ { 2 } } \cdot v _ { 2 } u _ { 2 } = \frac { 2 m _ { 1 } } { m _ { 1 } + m _ { 2 } } \cdot v _ { 1 } = \frac { 0,6 } { 0,5 } \cdot 3,381 = 4,057 m s ^ { - 1 }$$
$$\begin{array} { c } { \text { Nach dem StoB wird die kinetische Energie des Pendels mit Masse } m _ { 2 } \text { und der Pendellänge } L } \\ { \text { ausgelenkt und dabei der wird der Schwerpunkt um } h \text { angehoben. Es gilt: } } \\ { \frac { 1 } { 2 } m _ { 2 } u _ { 2 } ^ { 2 } = m _ { 2 } g h } \end{array}$$
warum wird Ekin=Epot ?
es müsste doch Erot=Epot
die Kugel hängt an einem Faden und bewegt sich daher auf einer Kreisbahn, so hat man es mir gesagt.