Berechnung der Dämpfungskonstante

Question

Guten Abend, ich komme bei folgenden Aufgaben nicht weiter

Aufgabe: Die Aufgabe ist auf der fünften Seite, die davorigen Seiten sind Erklärungen allgemein zum Thema.

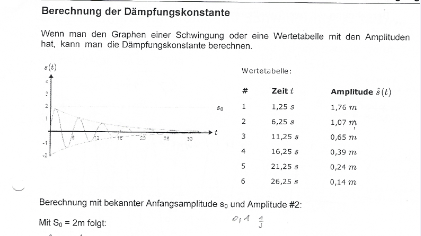
1.)Man soll mit den gegebenen Tabellen auf der fünften Seite die Dämpfungskonstante berrechnen und dann noch eine 2.)zusätzliche Aufgabe: Berechnung mit zwei Tabellenwerten aus Seite 5. Die Seiten 1 bis 4 sind nur Allgemeinwissen die man eventuell zur Aufgabe braucht.

1.)Problem/Ansatz:Seite 5: Berrechnung der Dämpfungskonstane-> Ansatz: s(t) = A*e^-k*t    

und dann nach k umstellen mit logarithmus

2.)zusätzliche Aufgabe: Berechnung mit zwei Tabellenwerten aus Seite 5.

z.B smax 1 -smax 2=A*e-k*t              ( smax 1 und smax 2 sind s dach aus der Tabelle S.5)

S.1 Wissen:

 

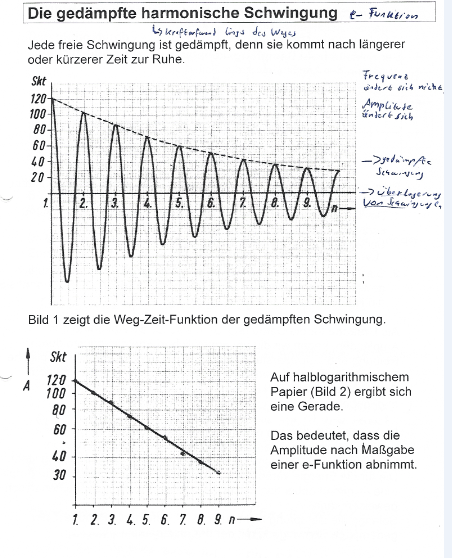
S.2 Wissen:

S.3 Wissen

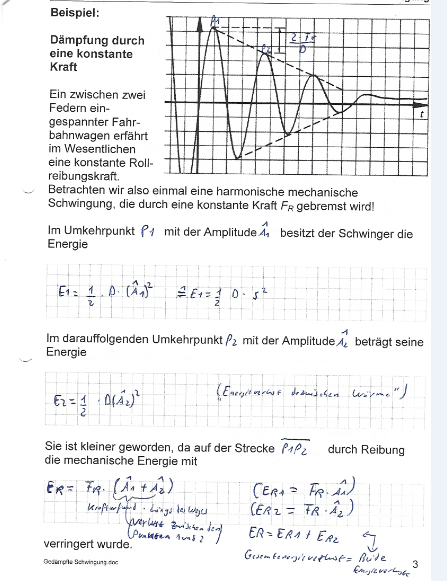
S.4 Wissen

S.5 Aufgabe und zusätzliche Aufgabe mit zwei Tabellenwerten (siehe oben)->2.)zusätzliche Aufgabe: Berechnung mit zwei Tabellenwerten aus Seite 5.

z.B smax 1 -smax 2=A*e-k*t              ( smax 1 und smax 2 sind s dach aus der Tabelle S.5)

S.5 

 

Answer 1

Hallo

s(t)=A*e^(-rt)*sin(2π/t*T)  s=A  für sin(2π/t*T)=1; also für T/2 und 3/2T In Tabelle ist T=5s

 also hast du s(3/2T)/s(T/2)=Ae^(-r*3T/2)/A*e^(-r*T/2) =1*e^(-r*T).  Zwei aufeinanderfolgene Amplituden entnimmst du der Tabelle und hast dann s₂/s₁=e^(-r*T) und findest r durch anwenden von ln. (die Differenz der Werte hilft dir nichts)

anderer Weg du trägst ln oder log A gegen t auf wie unter Bild 1 und bestimmst daraus r.

 da die Amplituden Fehlerbehaftet sind, ergeben sich abweichende Werte für r. ob ihr eine Fehlerrechnung machen sollt weiss ich nicht.

Gruß lul

Comments

Hallo, tut mir leid für meine späte Reaktion ich musste den Lehrer nochmal fragen ob ich es richtig verstanden habe-> wir  haben keine Fehlerberechnung gelernt-> also für die Amplituden.

Danke für die Ansätze leider habe ich die Aufgaben falsch verstanden, bei der 1.) Aufgabe soll man mit so = A= 2m und dem ersten Tabellenwert smax 1= 1,76m ,      t1= 1,25 s  arbeiten und in die Formel setzen und kürzen um auf die Dämpfungskonstante k zu kommen.

Bei der 2. ) Aufgabe mit  smax 1= 1,76m t1= 1,25s und smax 2= 1,07 m und t2= 6,25 s  also zwei Tabellenwerten arbeiten um wieder auf die Dämpfungskonstante k zu kommen. Man kann natürlich auch smax 2= 1,07m und smax 3= 0,65m nehmen usw. um auf k zu kommen.

So habe ich beide Aufgaben jetzt gelöst:

Aufgabe 1:

Aufgabe 2: