Hallo,
Bei dieser Aufgabe ist einiges durcheinander gekommen. Der Aufgabentext und das Schaltbild sind widersprüchlich. Denn das Schaltbild zeigt den Einschaltvorgang, der Text beschreibt aber den Ausschaltvorgang. Das kann man sich anhand der Gleichungen für den Einschaltvorgang und Ausschaltvorgang klarmachen:
Die Gleichung für das Bild oben, also für den Einschaltvorgang lautet:
$$i(t) = I_{max}*(1 - e^{- \frac{t}{τ}})$$
mit \(τ = \frac{L}{R} \) und \(I_{max} = \frac{U}{R}\)
für t = t0 ist i = 0
Selbst wenn man vermutet, dass der Schalter zum Zeitpunkt t = t0 geöffnet wird, ist der Strom ebenfalls Null, da bei geöffnetem Schalter kein Strom fließen kann. Das Schaltbild oben passt also nicht zum Aufgabentext. Folglich muss es sich um den Ausschaltvorgang handeln.
Hier das Schaltbild für den Ausschaltvorgang:
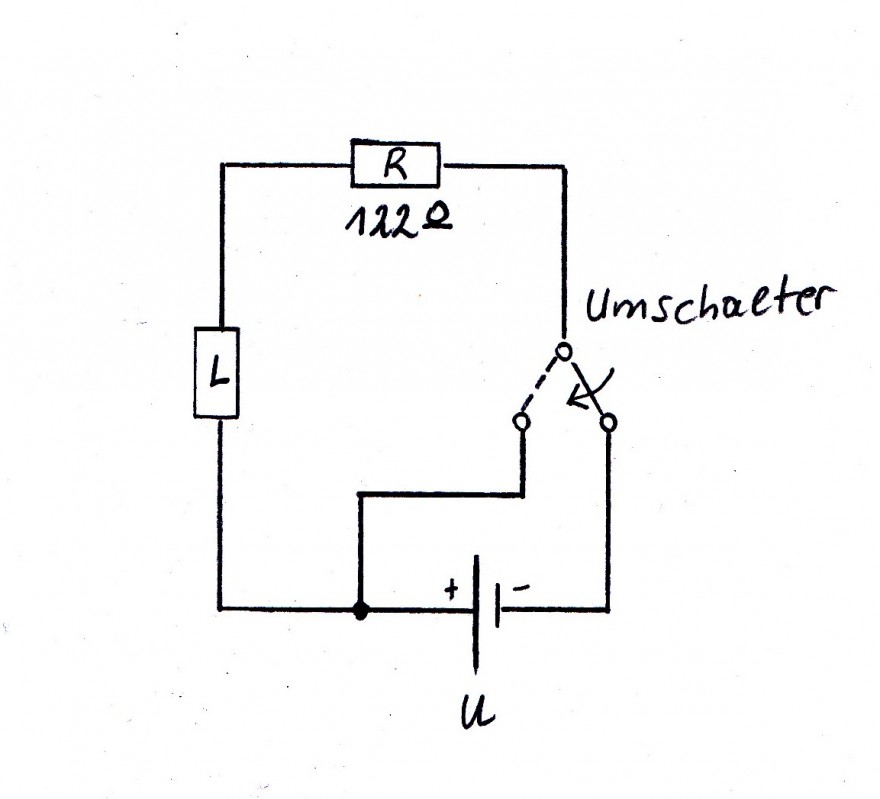
Die Gleichung für den Ausschaltvorgang lautet:
$$i(t) = I_{max}*e^{- \frac{t}{τ}}$$
Für t = t0 ist i = Imax = U/R
Die Berechnung für die gesuchte Induktivität wurde von georgborn bereits durchgeführt. Als Ergebnis erhält man:
$$L = 196,14 µH$$
Zum Schluss noch eine Frage für die Spezialisten: Würde man den Schalter öffnen ohne den Stromkreis zu schließen, also statt dem Umschalter wäre nur ein Öffner vorhanden, stellt sich die Frage, was mit der magnetischen Energie passiert, die in der Induktivität gespeichert ist. Irgendwo muss sie hin, aber wohin?
Hier noch eine kleine Ergänzung:
Das von mir eingestelle Schaltbild mit dem Umschalter zeigt das korrekte Schaltbild des Ausschaltvorgangs. Befindet sich der Umschalter in der rechten Schalterstellung, also mit der Spannungsquelle U, wird nach langer Einschaltzeit (also im eingeschwungenen Zustand) in der Induktivität eine magnetische Energie der Größe
\(W_{mag} = \frac{1}{2}*L*I_{max}^{2} \) aufgebaut.
Wir danach der Umschalter nach links umgelegt und der Stromkreis geschlossen, fließt ein Strom, wie im Aufgabentext angegeben, d.h. vom Maximalwert Imax beginnend nach der e-Funktion abnehmend. Die gesamte magnetische Energie, die in der Induktivität steckt, wird in dem Widerstand R in Wärme umgesetzt. Würde man den Stromkreis mit einem Öffner einfach unterbrechen und den Stromkreis nicht schließen, würde die magnetische Energie auf anderem Weg abgebaut werden, der nicht gewünscht ist und u.U. Probleme bereiten kann.
Gruß von hightech