Hallo,
Wie soll ich das rechen?
Bevor Du irgendwas rechnest, solltest Du Dir darüber klar werden, wie die beschriebenen Verhältnisse von Kräften und Winkeln überhaupt sind. Das geht am besten mit einer Skizze
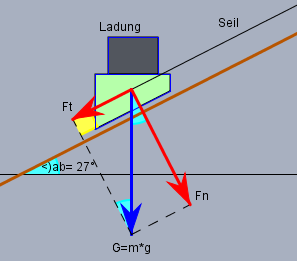
Auf einer schiefen Ebene steht ein Wagen samt Ladung, der von einem Seil gezogen wird. Das Seil wird parallel zur schiefen Ebene angenommen. Wagen und Ladung haben eine Masse \(m\), die im Schwerefeld der Erde zu einer Gewichtskraft \(G=m \cdot g\) führt. Die Gewichtkraft (blau) teilt sich bei den gegebenen Verhältnissen in eine Kraft \(F_n\) die senkrecht (also normal) auf die Ebene drückt und eine Kraft \(F_t\) (tangential) die auf das Seil wirkt, welches den Wagen zieht. Diese beiden Kräfte (rot) stehen senkrecht zueinander. Der Winkel von \(27°\) findet sich jeweils an den hellblau markierten Stellen wieder. Der gelb markierte Winkel ist ein rechter und bildet zusammen mit \(G\) und \(F_n\) ein rechtwinkliges Dreieck.
Demnach ist
$$F_t = G \cdot \sin(27°)$$
Damit die zulässige Seilkraft von 5000N nicht überschritten wird, muss gelten
$$F_t = m \cdot g \cdot \sin(27°) \lt 5000\text{N} \quad \Rightarrow m \lt \frac{5000\text{N}}{g \cdot \sin(27°)} \approx 1123 \text{kg}$$
D.h. die Gesamtmasse von Wagen und Ladung darf den oben angegebenen Betrag nicht überschreiten.