Beschleunigen Physik berechnen

Question

Verstehe die Aufgabe 3 die a und b nicht

Answer 1

Vielleicht geht es auch ohne Skizze.

das Boot wird auf den 120 m mit 0,8 m/s vom
Fluß mitgenommen. Die Zeit ist
120 = 0.8 * t
t = 150 sec

In dieser Zeit muß das Boot die 40 m zum anderen
Ufer in t erreicht haben
40 = v(Boot) * 150
v(Boot) = 40 / 150 = 0.267 m/s

Comments

Ich beginne und ende an der Fangstelle.
( der Fragetext ist nicht ganz eindeutig ).

Geschwindigkeit Boot = vb
Geschwindigkeit stromaufwärts vb - 0.8
Geschwindigkeit stromabwärts vb + 0.8
Strecke auf- oder abwärts = 1500 m
Zeit aufwärts = 15 min

Aufwärts : 1500 = ( vb - 0.8 ) * 15
Abwärts : 1500 = ( vb + 0.8 ) * x

Etwas für dich zum rechnen
Die erste Gleichung nach vb umstellen
und vb dann in die 2.Gleichung einsetzen
ergibt x ( Zeit für die Rückfahrt )

---

Aufwärts : 1500 = ( vb - 0.8 ) * 15
Abwärts : 1500 = ( vb + 0.8 ) * x
Korrektur:
da es heißt 0.8 m/s
muß es auch
Aufwärts : 1500 = ( vb - 0.8 m/s ) * 900 sec
Abwärts : 1500 = ( vb + 0.8 m/s ) * x sec
heißen

Answer 2

Hallo Maria,

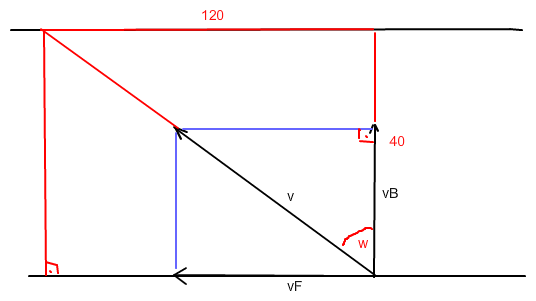
a)

tan(w) = 120/40 = 3 = vF / vB    →  vB  = 1/3 * vF   =  1/3 * 0,8 m/s  ≈ 0,267 m/s

[Die Gleichung  ergibt sich auch aus dem 2. Strahlensatz oder der Ähnlichkeit der Dreiecke]

b)

t in Sekunden, s in Meter , Geschwindigkeiten in m/s

  x = Eigengeschwindigkeit des Bootes bei Vollgas 

Flussaufwärts:

s = v * t   →    1500 = ( x - 0,8) * 900  →   x ≈ 2,47  

Flussabwärts:

t  ≈  s / (x+0,8)  ≈ 1500 / (2,47+0,8)  ≈  458   [Sekunden] 

      ≈  7,63 Minuten  ≈  7 Minuten 46 Sekunden.

Gruß Wolfgang